非線形制御でお世話になるフロベニウスの定理を理解するのが最終目的であるが,その第一ステップとしてベクトル場のディストリビューションが作る積分多様体について色々調べていた時のメモ.
ベクトル場から曲面を作れないか?
いくつかの文献を読んでいて感じたのは,積分多様体とか involutive とかいったものは,材料となる複数のベクトル場を 重ねあわせて (合成して?)曲面を構成できるか,という問題意識のもとで語られているようだということである.大雑把には
与えられたベクトル場Vに対して,曲面上の全ての点において,(その点での)Vのベクトルが曲面に接している
ように「重ね合わせる」イメージ.ベクトル場Vの積分曲線を「積み重ねていけば」このような曲面を構成できることは想像できる.例えば以下の円環状に分布しているベクトル場を見てみると,
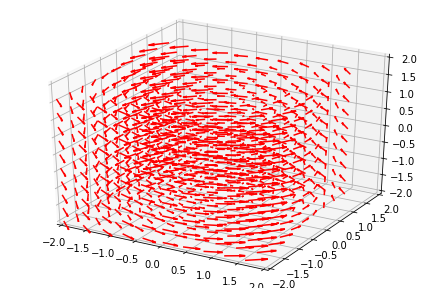
この場合は半径rの積分曲線が各z平面において存在しているので,この積分曲線を「積み重ねた」円柱はその表面においてベクトル場が円柱に接しており,上の条件を満たす曲面になっていることが分かる.
より一般的に複数のベクトル場 $V_1, V_2, \cdots, V_m$ を考えて
与えられたベクトル場 $V_1, V_2, \cdots, V_m$ に対して,その曲面上の全ての点において $V_1, V_2, \cdots, V_m$ たちがその曲面に接している
ような曲面を構成することができるかという問題を考える.
そのような曲面が満たすべき条件
そのような曲面があったとして,その表面に各ベクトル場が接しているということは,そのとき曲面の 法線ベクトル はベクトル場 $V_1, V_2, \cdots, V_m$ の全てに直交している はずである.そこで求める曲線の方程式を $f(x_1, x_2, \cdots, x_n)$ とすると
$$ df = \dfrac{\partial f}{\partial x_1}dx_1 + \cdots + \dfrac{\partial f}{\partial x_m}dx_m $$
より法線ベクトルの成分は $(\partial f / \partial x_1, \cdots, \partial f / \partial x_m)$.また各ベクトル場を
$$ V_i = V_{i}^1 \dfrac{\partial}{\partial x_1} + \cdots + V_{i}^n \dfrac{\partial}{\partial x_m} $$
と定義すると,これらの内積がゼロ,すなわち
$$ df \left( V_i \right) = 0, \quad \text{for all $i$} $$
が成立しているはずである.
3次元における具体例
例として以下のような2つのベクトル場X,Yのディストリビューションの積分多様体を求めてみる.
$$\begin{align*} X &= -y \dfrac{\partial}{\partial x} + x \dfrac{\partial}{\partial y} \\ Y &= (x - y)z \dfrac{\partial}{\partial x} + (x + y)z \dfrac{\partial}{\partial y} + (1 + z^2) \dfrac{\partial}{\partial z} \end{align*}$$
$X$ は上で示した円環状のベクトル場,$Y$ は以下に示すようなベクトル場である.
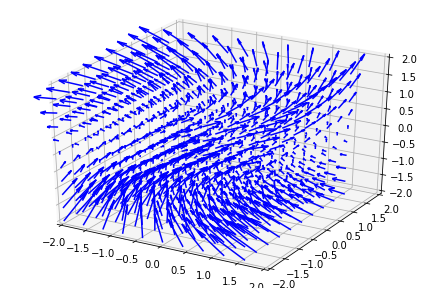
求める関数の全微分を1形式 $\omega = df = a dx + b dy + c dz$ とする($a, b, c$ は関数).ベクトル場と内積をとると
$$\begin{align*} & \omega (X) = -ay + bc = 0 \\ & \omega (Y) = a(x -y)z + b(x + y)z + c(1 + z^2) = 0 \end{align*}$$
が得られ,第1式から $a = c, b = y$ とおくと,第2式より
$$ c = -\dfrac{x^2 + y^2}{1 + z^2}z $$
となる.第1,2式ともに$=0$なので, $a, b, c$ を $x^2 + y^2$ で割って
$$ \omega = \dfrac{x}{x^2 + y^2}dx + \dfrac{y}{x^2 + y^2}dy - \dfrac{z}{1 + z^2}dz $$
とする.これは全微分になっていて,
$$ f(x, y, z) = x^2 + y^2 - c(1 + z^2) = 0 $$
が解の曲面となる.
確認
この関数の法線ベクトルは
$$ \boldsymbol{n} = (2x, 2y, -2cz) $$
であり.X,Yとの内積は
$$\begin{align*} & 2x \cdot (-y) + 2y \cdot (x) = 0 \\ & 2x \cdot (x - y)z + 2y \cdot (x + y)z - 2cz \cdot (1 + z^2) = 2(x^2 + y^2)z - 2cz(1 + z^2) = 0 \end{align*}$$
となっている.よってこの曲面の法線ベクトルは 全ての点においてX,Y両方に直交している .あるいはこの曲面上のあらゆる曲線におけるあらゆる速度ベクトルは,X,Yの線型結合になっている.より数学的にいうならば,この積分多様体の接バンドル $\mathrm{T} M$ は, $M$ 上に制限した $X, Y$ を部分集合として持つようになっている.