読んでいて詰まったところをメモっていく.
1.1 多項式曲線フィッティング
教科書では $\sin (2 \pi x)$ に従うランダムデータを多項式でフィッティングする例題を用いている.
$$\begin{align*} y(x, \boldsymbol{w}) = w_0 + w_1 x + w_2 x^2 + \cdots + w_M x^M \end{align*}$$
基本的にモデルの次数は $3 < M < 8$ ぐらいが良さそうに見える.$M =9$ においてはデータ点数10に対して多項式の重みも10個あるため,すべてのデータ点を通るよう誤差が0となるフィッティングが行えている.しかしむちゃくちゃに発散した曲線となっており,ランダムに生成したテストデータのバッチに対しては誤差が大きくなると想定される.
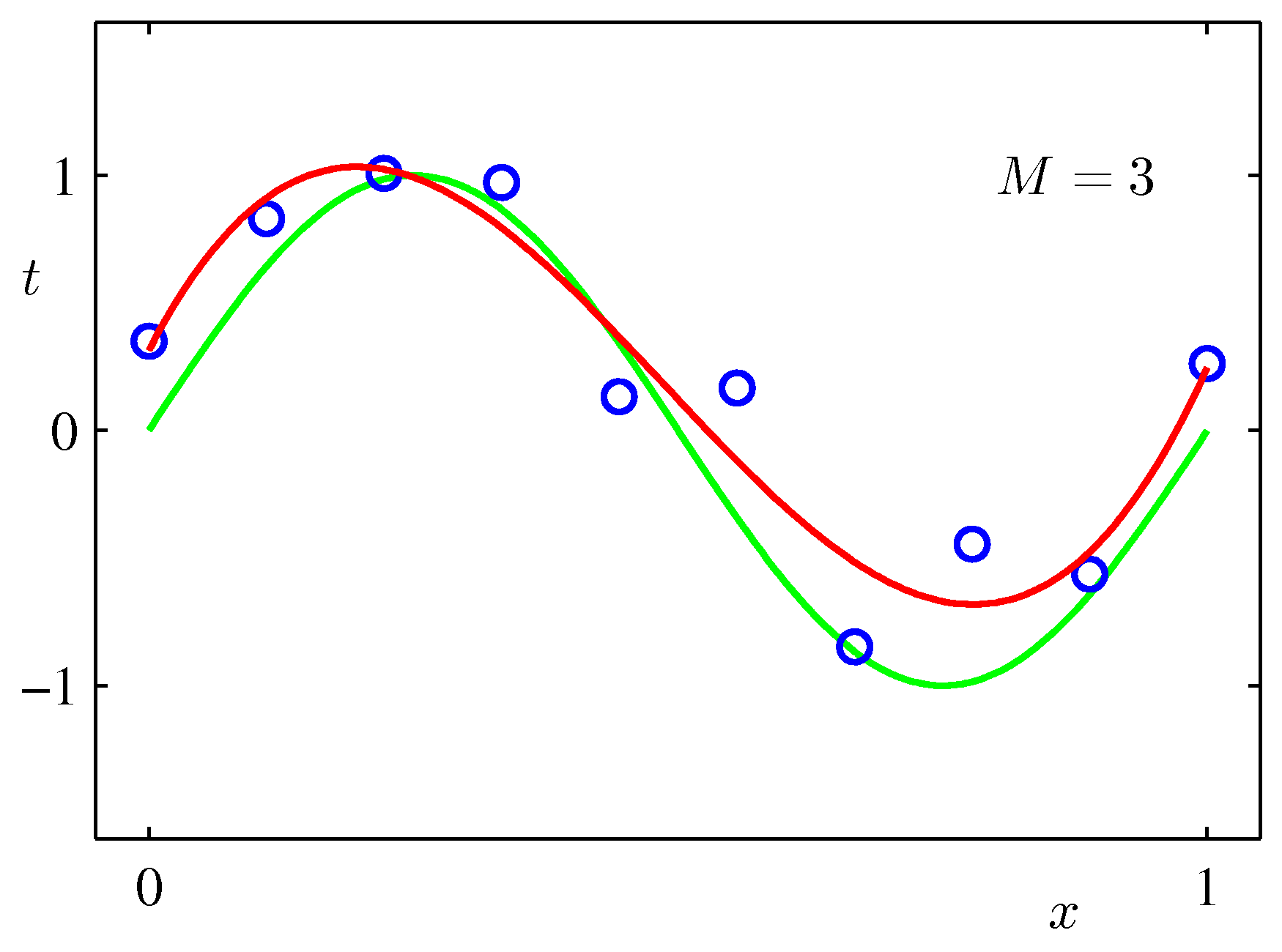
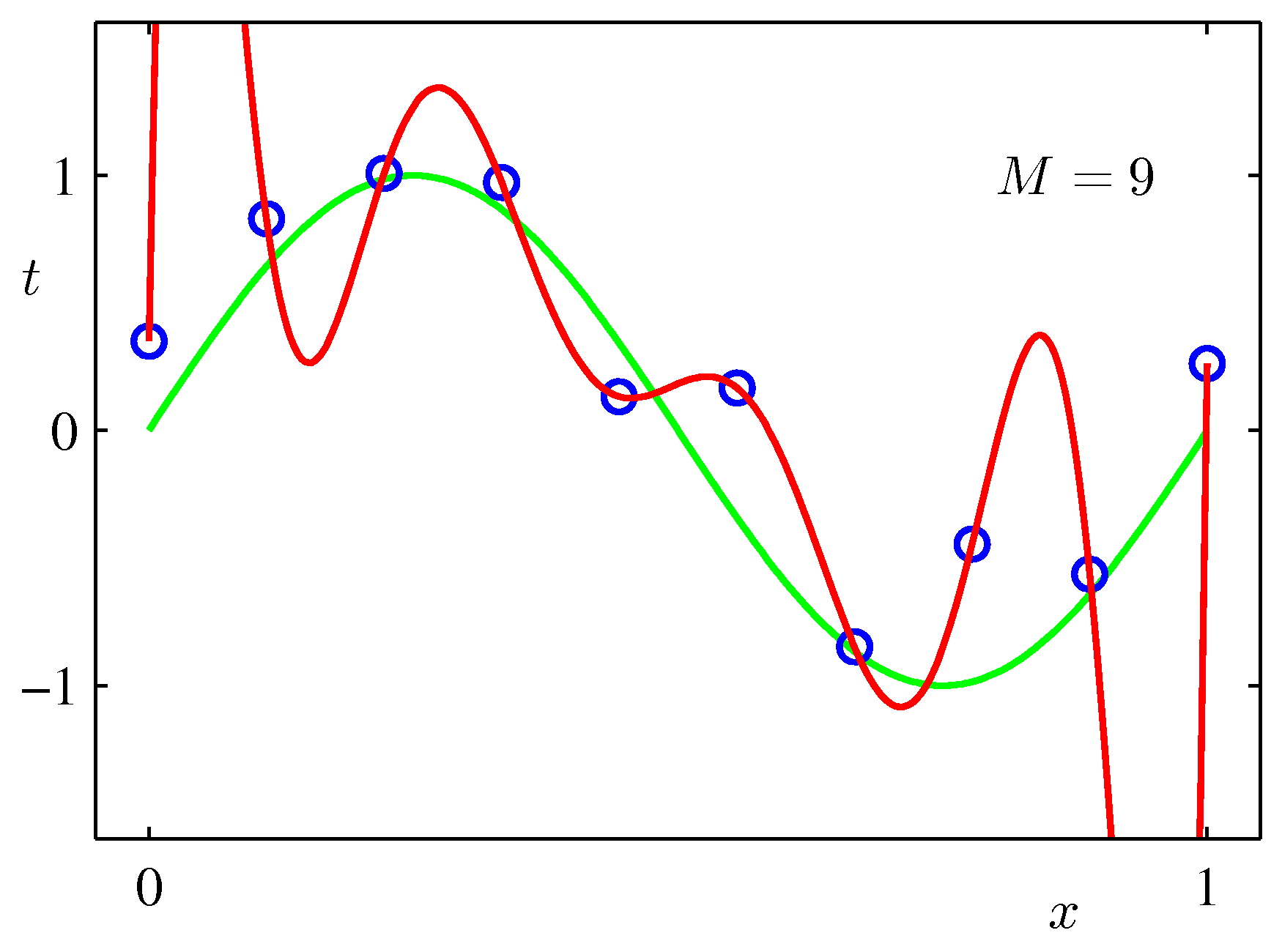
一方でモデルの次数が高くても,データ集合のサイズが大きければ過学習はそれほど深刻ではなくなる.
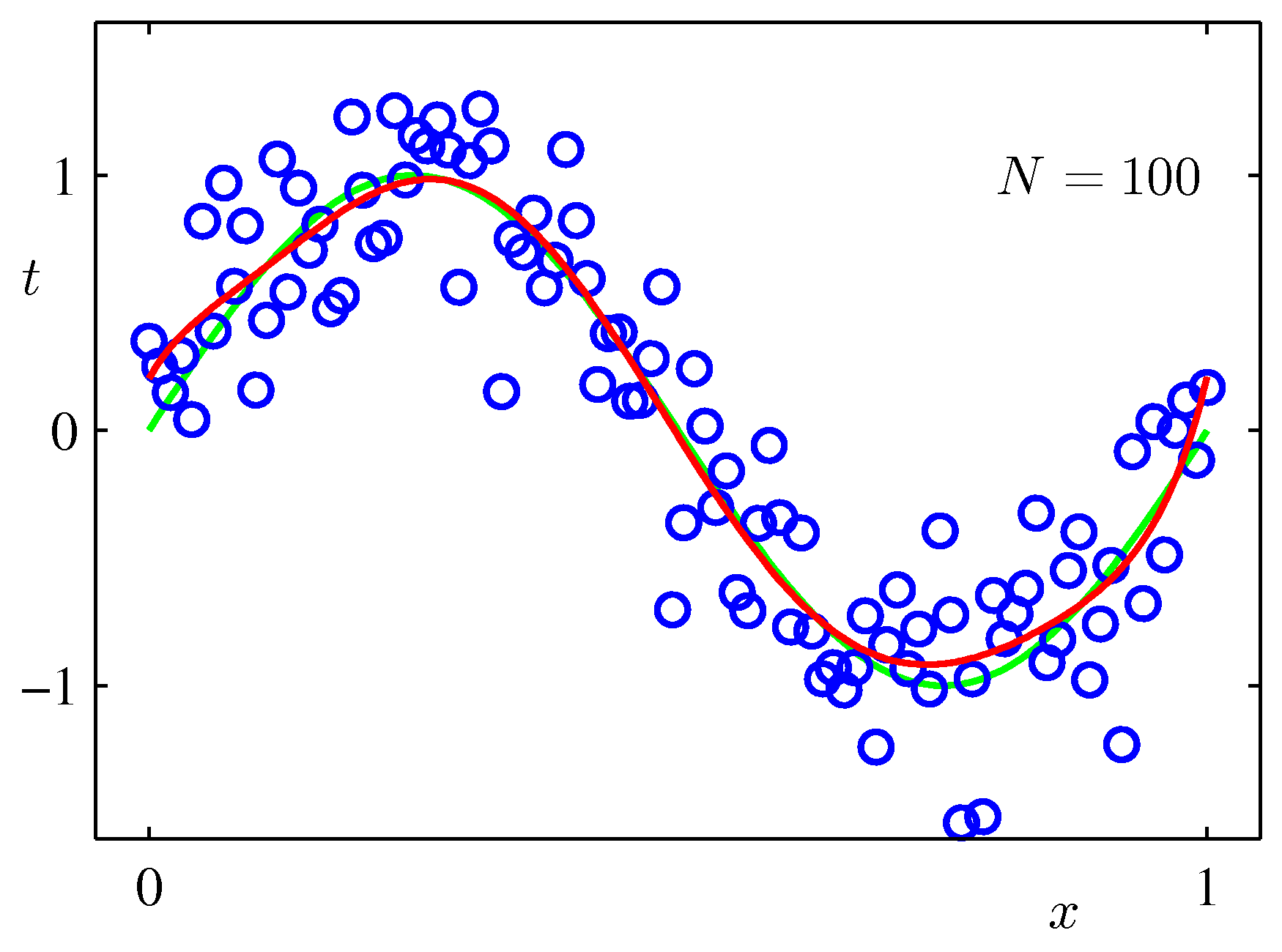
しかし,入手できるデータ集合のサイズに応じてモデルの次数を調整しなければならないのは不自然ではないだろうか?結局のところそのデータの生成源にはそれに特有のモデルの次数が存在するのであろうし,モデル次数がその時点で得られているデータ集合のサイズに依存するわけがない.その生成源からのデータが多かろうと少なかろうと(真に必要な,重要な)パラメータは必要であろうし,せめてデータ集合のサイズに応じてパラメータ数を調整できないだろうか?
過学習の問題は最尤推定に特有であるが,ベイズ的アプローチを採用すれば回避することができる.ベイズのアプローチではモデルの次数(パラメータ数)がデータ集合のサイズを大幅に超えていてもよく,パラメータ数はデータ集合のサイズによって自動的に決定される(らしい).
過学習の問題を避けるテクニックとして正則化も有名である.
$$\begin{align*} \tilde{E}(\boldsymbol{w}) = \dfrac{1}{2} \sum_{n=1}^{N} (y(x_n, \boldsymbol{w}) - t_n)^2 + \dfrac{\lambda}{2} | \boldsymbol{w} |^2 \end{align*}$$
先ほどの9次の多項式フィッティングにおいて正則化を用いた結果が下の図のようになる.
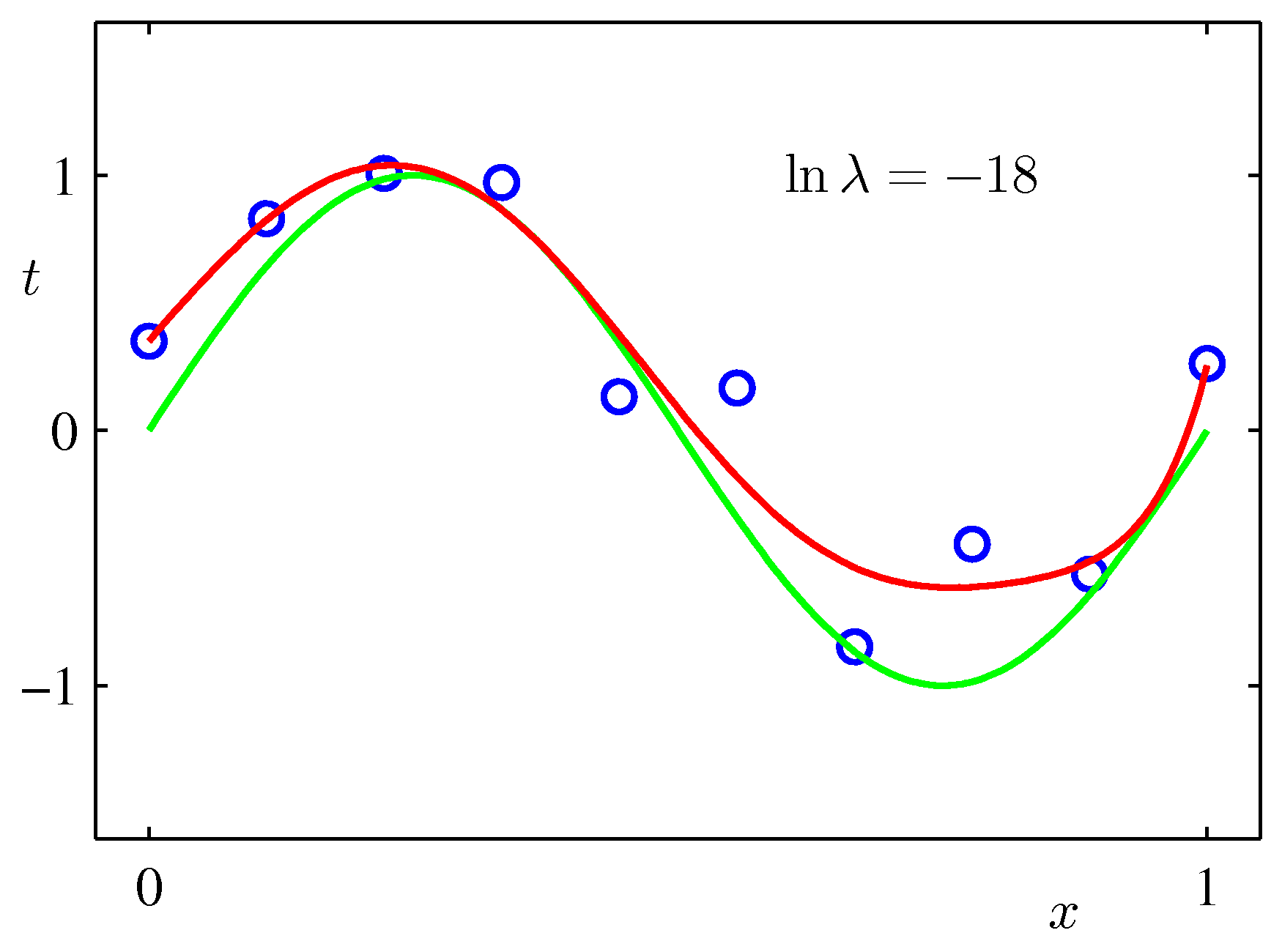
1.2 確率論
1.2.3 ベイズ確率
パラメータ $\boldsymbol{w}$ は不確実性を持った確率分布で表わされる量であり,データを観測するたびに分布が更新される. $$\begin{align*} p(\boldsymbol{w} \mid \mathcal{D}) =\dfrac{p(\mathcal{D} \mid \boldsymbol{w})p(\boldsymbol{w})}{p(\mathcal{D})} \end{align*}$$
- $p(\boldsymbol{w})$ は $\boldsymbol{w}$ の事前分布である
- $p(\mathcal{D} \mid \boldsymbol{w})$ は $\boldsymbol{w}$ の関数であり,尤度関数と呼ばれている.これは $\boldsymbol{w}$ で積分しても1にならないので,確率分布ではない.$\boldsymbol{w}$ を用いて得られたデータ $\mathcal{D}$ を評価するものである.
- $p(\boldsymbol{w} \mid \mathcal{D})$ は $\boldsymbol{w}$ の事後分布であり,観測データ $\mathcal{D}$ の関数である,つまり $\mathcal{D}$ により確率分布が変化したものである.
頻度主義で用いられる最尤推定はこの尤度関数 $p(\mathcal{D} \mid \boldsymbol{w})$ を最大化するものである.
1.2.4 ガウス分布
多変数では一般に以下のような密度関数となる.
$$\begin{align*} \mathcal{N}(\boldsymbol{x} \mid \boldsymbol{\mu}, \Sigma) = \dfrac{1}{\sqrt{\det (2 \pi \Sigma)}} \exp \left( -\dfrac{1}{2}(\boldsymbol{x} - \boldsymbol{\mu})^{\text{T}}\Sigma^{-1}(\boldsymbol{x} - \boldsymbol{\mu}) \right) \end{align*}$$
一変数の場合にパラメータを最尤推定すると
$$\begin{align*} \mu_{\mathrm{ML}} &= \dfrac{1}{N} \sum_{n=1}^{N} x_n \\ \sigma^2_{\mathrm{ML}} &= \dfrac{1}{N} \sum_{n=1}^{N} (x_n - \mu_{\mathrm{ML}})^2 \end{align*}$$
となる.これらの量はデータの関数である.そこでデータについて期待値をとってみると
$$\begin{align*} \mathbb{E}[\mu_{\mathrm{ML}}] &= \mu \\ \mathbb{E}[\sigma^2_{\mathrm{ML}}] &= \left( \dfrac{N-1}{N} \right) \sigma^2 \end{align*}$$
となる.標本分散が実際より分散を過小評価してしまう理由を以下に述べよう.
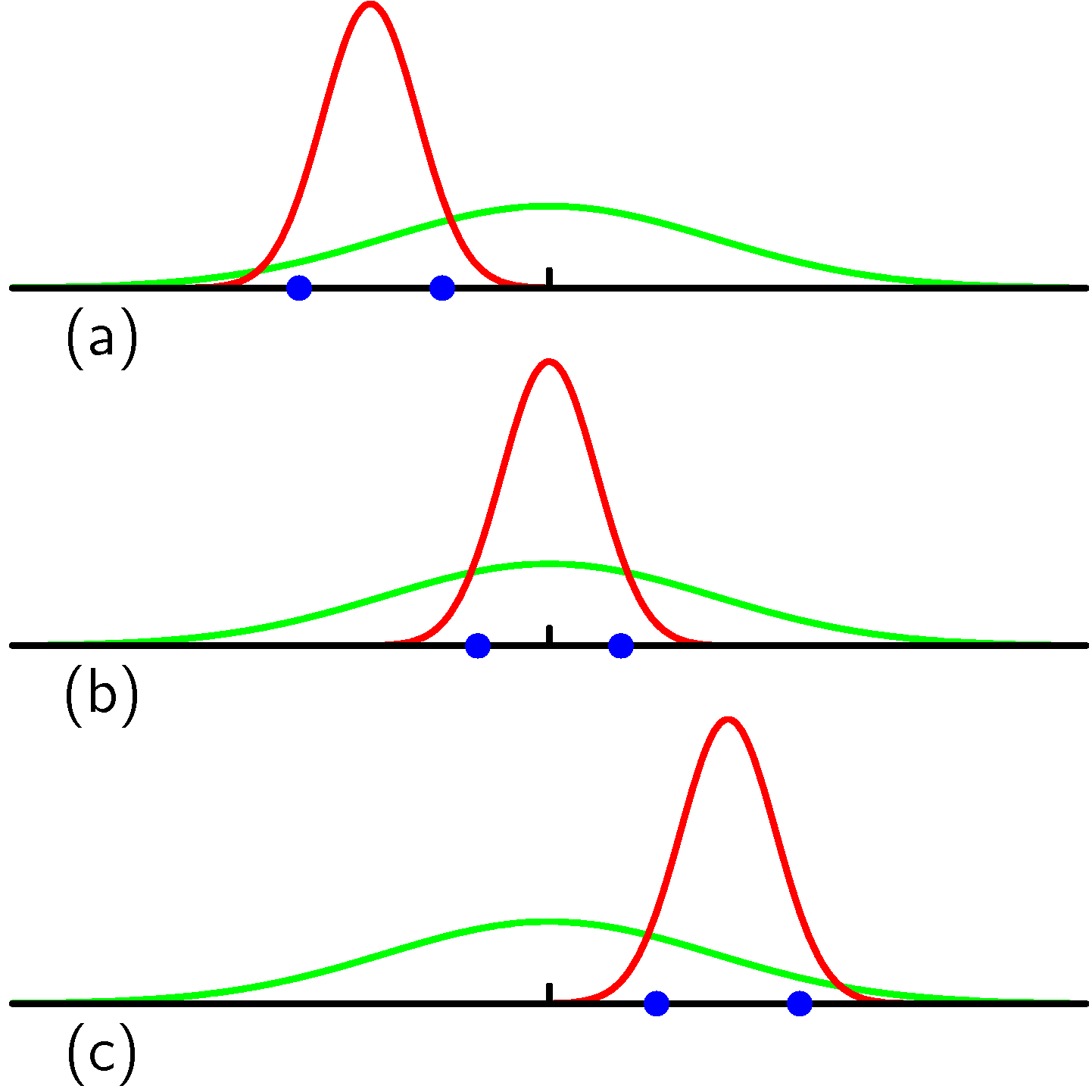
実際にデータを収集する以上,図の緑色のガウス分布から得られたデータはどうしても $\pm 3 \sigma$ 付近に集中してしまう.そして裾野からはあまりデータが得られない.そのため最尤推定でフィッティングした分布は,緑色のガウス分布の $\pm 3 \sigma$ 付近に集中したガウス分布になってしまう.裾野の方のデータがあまり得られないため,もとのガウス分布ほどには広がってくれないのである.このようにして平均的には標本分散はもとの $\sigma$ より小さくなってしまうのである.
1.5 決定理論
例題として医療診断問題が挙げられている.この場合入力ベクトル $\boldsymbol{x}$ はX線画像であり,出力は癌であるかないかのクラス $C_1$, $C_2$ である.
$$\begin{align*} p(\mathcal{C}_k \mid \boldsymbol{x}) = \dfrac{p(\boldsymbol{x} \mid \mathcal{C}_k) p(\mathcal{C}_k)}{p(\boldsymbol{x})} \end{align*}$$
ここで $p(\mathcal{C}_k)$ はクラス分類の事前分布(世の中一般的に癌にかかるかかからないか,X線検査を受ける人間が癌にかかっている確率),$p(\boldsymbol{x} \mid \mathcal{C}_k)$ はその診断画像が癌で{ある,ない}それぞれの尤度である.
1.5.4 推論と決定
クラス分類を解くアプローチとしてはi)訓練データからモデル $p(\mathcal{C}_k \mid \boldsymbol{x})$ を学習する推論を行ってから事後確率を使ってクラス割り当ての決定を行う(識別モデル),ii)入力から直接決定関数を学習する(生成モデル),の二つのアプローチがある.
識別モデル 最初に出力の事後確率 $p(\mathcal{C}_k \mid \boldsymbol{x})$ を求める.
生成モデル 最初に入力の条件付き密度 $p(\boldsymbol{x} \mid \mathcal{C}_k)$ を求める.そしてベイズの定理により $$\begin{align*} p(\mathcal{C}_k \mid \boldsymbol{x}) = \dfrac{p(\boldsymbol{x} \mid \mathcal{C}_k) p(\mathcal{C}_k)}{p(\boldsymbol{x})} \end{align*}$$ を求める.分母の密度関数は $$\begin{align*} p(\boldsymbol{x}) = \sum_k p(\boldsymbol{x} \mid \mathcal{C}_k) p(\mathcal{C}_k) \end{align*}$$ により求められる.このように入力の分布もモデル化するアプローチは,モデルからのサンプリングにより入力空間で人口データを生成できることから(???まだ意味が分からない)生成モデルと呼ばれる.
識別関数 入力 $\boldsymbol{x}$ から出力を得る2値関数 $f(\boldsymbol{x}) = 0, 1$ を構成する.
生成モデルのアプローチは(多くの場合高次元データである) $\boldsymbol{x}$ の分布を求める必要があるため,多くの訓練集合と計算資源が必要になってしまう.しかし生成モデルでは与えられたデータ $\boldsymbol{x}$ についてその周辺分布 $p(\boldsymbol{x})$ を求めることができるため,もしあるデータの値 $p(\boldsymbol{x}_0)$ が小さければ,それは現在のクラス割り当てにおいて外れ値とみなされるべきであると推論することができる.
識別関数を構成するアプローチだと事後確率 $p(\mathcal{C}_k \mid \boldsymbol{x})$ がもはや分からない.最終的に決定を下す場合にしても(リスク的な意味合いで)事後確率を計算したくなる.
モデルの結合
癌の診断を行う先ほどの具体例では,X線画像(x1)のほかに血液検査の結果(x2)も利用できるかもしれない.しかしこれらの入力をまとめるよりは,それぞれを個別に扱った後に統合したほうが良い.そのための単純な方法としてはx1,x2が独立であるという仮定を置いて
$$\begin{align*} p(\boldsymbol{x}_a, \boldsymbol{x}_b \mid \mathcal{C}_k) = p(\boldsymbol{x}_a \mid \mathcal{C}_k) p(\boldsymbol{x}_ \mid \mathcal{C}_k) \end{align*}$$
を用いることにより
$$\begin{align*} p(\mathcal{C}_k \mid \boldsymbol{x}_1, \boldsymbol{x}_2) &\propto p(\boldsymbol{x}_1, \boldsymbol{x}_2 \mid \mathcal{C}_k)p(\mathcal{C}_k) \\ &\propto p(\boldsymbol{x}_1 \mid \mathcal{C}_k) p(\boldsymbol{x}_2 \mid \mathcal{C}_k) p(\mathcal{C}_k) \\ &\propto \dfrac{p(\mathcal{C}_k \mid \boldsymbol{x}_1) p(\mathcal{C}_k \mid \boldsymbol{x}_2)}{p(\mathcal{C}_k)} \end{align*}$$
のようにそれぞれの事後確率から両者を統合した事後確率が得られる.条件独立の仮定はナイーブベイズと呼ばれている.
1.6 情報理論
エントロピーは密度関数に関する汎関数である.離散値に対してはエントロピーは
$$\begin{align*} H[x] = -\sum_x p(x) \log_2 p(x) \end{align*}$$
連続分布に対しては
$$\begin{align*} H[\boldsymbol{x}] = -\int p(\boldsymbol{x}) \ln p(\boldsymbol{x}) d\boldsymbol{x} \end{align*}$$
で定義される(微分エントロピー).
$\boldsymbol{x}$,$\boldsymbol{y}$ の2つの確率変数に対してそれらの条件付きエントロピーは
$$\begin{align*} H[\boldsymbol{y} \mid \boldsymbol{x}] = -\int \int p(\boldsymbol{y}, \boldsymbol{x}) \ln p(\boldsymbol{y} \mid \boldsymbol{x}) d \boldsymbol{y} d \boldsymbol{x} \end{align*}$$
1.6.1 相対エントロピーと相互情報量
ある未知の確率分布 $p(\boldsymbol{x})$ があってそれを別の確率分布 $q(\boldsymbol{x})$ で近似したとする.$p(\boldsymbol{x})$ からの信号を符号化する際に代わりに $q(\boldsymbol{x})$ を用いて符号化を行った場合,余分に
$$\begin{align*} \mathrm{KL}(p | q) &= -\int p(\boldsymbol{x}) \ln q(\boldsymbol{x}) d\boldsymbol{x} - (-\int p(\boldsymbol{x}) \ln p(\boldsymbol{x}) d\boldsymbol{x}) \\ &= -\int p(\boldsymbol{x}) \ln \left( \dfrac{q(\boldsymbol{x})}{p(\boldsymbol{x})} \right) d \boldsymbol{x} \end{align*}$$
だけビットが必要である.この量を相対エントロピーまたはKLダイバージェンスと呼ぶ.
$\boldsymbol{x}$,$\boldsymbol{y}$ について,もし独立であるならば
$$\begin{align*} p(\boldsymbol{x}, \boldsymbol{y}) = p(\boldsymbol{x})p(\boldsymbol{y}) \end{align*}$$
が成立する.そこで $\boldsymbol{x}$,$\boldsymbol{y}$ がどれほど独立でないかをKLダイバージェンスを用いて測るのが,以下の相互情報量である.
$$\begin{align*} I(\boldsymbol{x}, \boldsymbol{y}) = \mathrm{KL}(p(\boldsymbol{x}, \boldsymbol{y}) | p(\boldsymbol{x})p(\boldsymbol{y})) \end{align*}$$