ベイズ線形回帰はガウス分布の計算をすれば導出できるが.個人的にはエビデンス近似がこの章のキモ.
ベイズ線形回帰
入力 $\boldsymbol{x}$ に対して出力 $t$ をモデリングする.ここで訓練データを $\boldsymbol{X} = [\boldsymbol{x}_1, \cdots \boldsymbol{x}_N]$,$\boldsymbol{t}$ と表記する.データは真値を中心とするガウス分布
$$\begin{align*} t = y(\boldsymbol{x}, \boldsymbol{w}) + \epsilon \end{align*}$$
により生成されるとする.つまり
$$\begin{align*} p(t \mid \boldsymbol{w}, \beta) = \mathcal{N}(t \mid y(\boldsymbol{x}, \boldsymbol{w}), \beta^{-1}) \end{align*}$$
とする.よって得られたデータの尤度は
$$\begin{align*} p(\boldsymbol{t} \mid \boldsymbol{X}, \boldsymbol{w}, \beta) = \prod \mathcal{N}(t_n \mid \boldsymbol{w}^{\text{T}} \boldsymbol{\phi}(\boldsymbol{x}_n), \beta^{-1}) \end{align*}$$
である.
パラメータの分布
推定するパラメータ $\boldsymbol{w}$ について事前分布 $\mathcal{N}(\boldsymbol{w} \mid \boldsymbol{m}_0, S_0)$ を仮定する.すると先ほどの尤度関数との積をとって平方完成することで
$$\begin{align*} p(\boldsymbol{w} \mid \boldsymbol{t}_N) &= \mathcal{N}(\boldsymbol{m}_N, S_N) \\ \boldsymbol{m}_N &= S_N(S_0^{-1} \boldsymbol{m}_0 + \beta \Phi_N^{\text{T}}\boldsymbol{t}_N) \\ S_N^{-1} &= S_0^{-1} + \beta \Phi_N^{\text{T}}\Phi_N \end{align*}$$
が得られる.
具体例(重要)
図3.7の説明.直線 $y = w_0 + w_1 x$ を中心として $y = \mathcal{N}(y \mid w_0 + w_1 x, 0.2^2)$ からランダムに生成されたデータを用いて,係数 $w_0$ ,$w_1$ を学習したい.
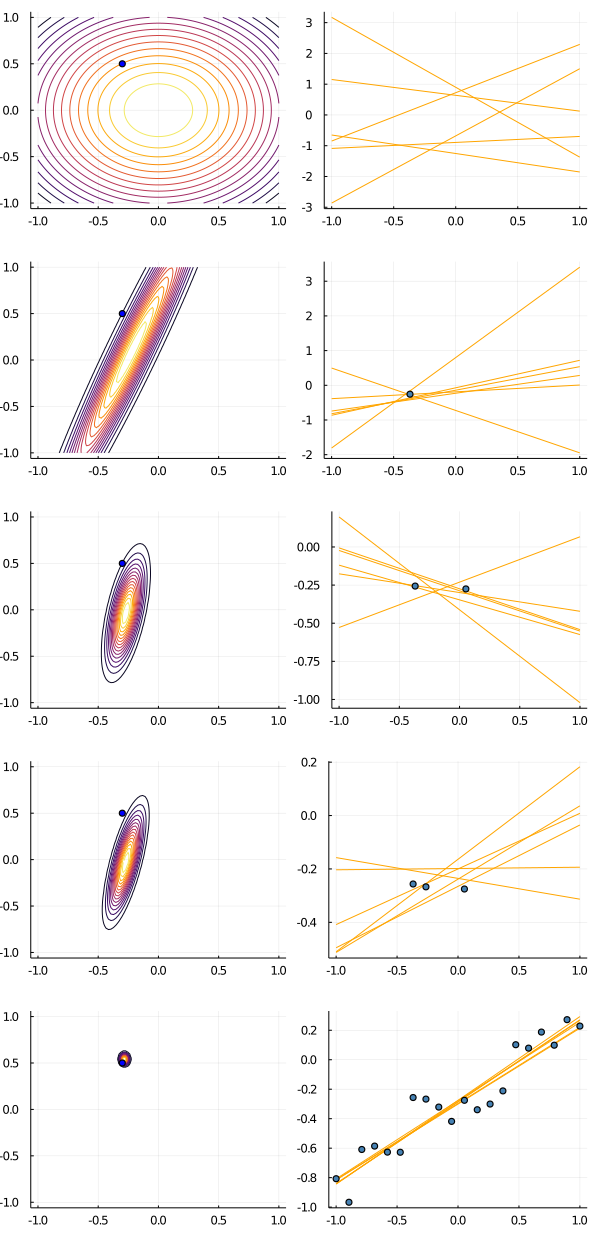
wの真値を(-0.3, 0.5)としてデータを生成する.もちろん学習アルゴリズムの側ではその真値は知らないので,はじめは図(1.2)のようにwは(0, 0)を中心とする分布に従うと仮定している.
次に図(2.3)のようにデータOが与えられると,それに応じて事後分布が図(2.2)のように変化する.この事後分布から生成したwを用いた直線は,少しづつデータの近くを通る直線に収束していく.
図(3.3)のようにさらにデータを追加すると,事後分布は図(3.2)のようにより小さくなっていく.その事後分布からランダムサンプリングしたwによる直線は,よりデータ点近くを通るようになっていく.
最終的にwの事後分布は図(4.2)のように真値(-0.3, 0.5)に収束していくことが分かる.このwの事後分布からドローして得られる直線は,学習データにフィッティングするような直線となることが分かる .
一連の様子を下の図に示す.
エビデンス近似
ハイパーパラメータ $(\alpha, \beta)$ についてもデータから推定を行う.式(3.74)は以下のようにして導出している.
$$\begin{align*} p(t \mid \boldsymbol{t}) &= \int p(t \mid \boldsymbol{w}, \alpha, \beta, \boldsymbol{t}) p(\boldsymbol{w}, \alpha, \beta \mid \boldsymbol{t}) d\boldsymbol{w} d\alpha d\beta \\ &= \int p(t \mid \boldsymbol{w}, \beta) p(\boldsymbol{w} \mid \boldsymbol{t}) d\boldsymbol{w} d\alpha d\beta \\ &= \int p(t \mid \boldsymbol{w}, \beta) p(\boldsymbol{w} \mid \boldsymbol{t}, \alpha, \beta) p(\alpha, \beta \mid \boldsymbol{t}) d\boldsymbol{w} d\alpha d\beta \end{align*}$$
正直なところ,この後の式(3.77)の導出には計算ミスがあるのではないかと思う.式(3.80)の平方完成において $\alpha$ , $\beta$ の項を定数項として足しているが,この項は式(3.89), (3.94)の偏微分に影響を与えるためだ.
アルゴリズム
- $\alpha \leftarrow \alpha_0$
- $\beta \leftarrow \beta_0$
- while $(\alpha, \beta)$ converges do:
- $\boldsymbol{m}_N \leftarrow \beta(\alpha I + \beta \Phi^{\text{T}}\Phi)^{-1}\Phi^{\text{T}}\boldsymbol{t}$
- $\boldsymbol{\lambda} \leftarrow \mathrm{eig}(\beta \Phi^{\text{T}}\Phi)$
- $\gamma \leftarrow \sum_i \lambda_i / (\alpha + \lambda_i)$
- $\alpha \leftarrow \gamma / ||\boldsymbol{m}_N ||$
- $1 / \beta \leftarrow \sum_{n=1}^{N}(\boldsymbol{m}_N^{\text{T}}\boldsymbol{\phi}(\boldsymbol{x}_n) - t_n)^2 / (N - \gamma)$
- end while
- return $(\alpha, \beta)$
有効パラメータ数
得られたデータに対する尤度関数 $p(\boldsymbol{t} \mid \boldsymbol{w})$ は $\boldsymbol{w}$ の関数となる.この関数は $\boldsymbol{w}_{\mathrm{ML}}$ (最尤推定値)を中心とし,等高線は楕円になる.2次形式の行列の固有ベクトルに沿って主軸が決まるのだが,その固有値が小さいほど楕円は固有ベクトルの方向に伸びる(半径が大きい).逆に固有値が大きいほど楕円はその固有ベクトルの方向には半径が小さい.
事前分布 $\mathcal{N}(\boldsymbol{w} \mid \alpha^{-1}I)$ を考慮すると,$\boldsymbol{w}_{\mathrm{ML}}$ が少しだけ原点の方向にシフトして $\boldsymbol{w}_{\mathrm{MAP}}$ が得られる.シフトする方向は,尤度関数において固有値が比較的小さい固有ベクトルの方向である.つまり等高線における楕円の長軸の方向にシフトしやすい.
固有値 $\lambda_i$,$\boldsymbol{u}_i$ が大きい場合,すなわち $\lambda_i \gg \alpha$ である場合 $\lambda_i / (\lambda_i + \alpha)$ は1に近くなる.このとき $\boldsymbol{w}_{\mathrm{ML}} \rightarrow \boldsymbol{w}_{\mathrm{MAP}}$ はこの $\boldsymbol{u}_i$ の方向にはあまりシフトしない.つまり $w_i$ はデータから決定される度合いが強いと言えそうである.これをwell-determinedパラメーターという.
一方で $\lambda_i$ が小さい場合は先ほど述べたように,$\boldsymbol{w}_{\mathrm{ML}} \rightarrow \boldsymbol{w}_{\mathrm{MAP}}$ において $\boldsymbol{u}_i$ の方向へのシフトが比較的大きい.つまりデータを観測しても $w_i$ は事前分布の方向に引き寄せられるということである(この重みパラメーターはどれだけデータを観測しても,結局事前分布の値に近くなる).
よって $\gamma = \sum_i \lambda_i / (\lambda_i + \alpha)$ はwell-determinedパラーメーターの個数を表している.
なぜ初めに重みパラメーターの初期値を0にしたのか
ここにきてなぜ初めに事前分布として平均が0の $\mathcal{}(\boldsymbol{w} \mid 0, \alpha^{-1}I)$ を採用したのかが分かる.結果からいうと,undeterminedなパラメーターの値を自動的にゼロにするためである.
教科書において,三角関数から生成されたデータを $\boldsymbol{w}^{\text{T}}\boldsymbol{\phi}(\boldsymbol{x})$ でフィッティングする例題が繰り返し用いられている.ここではパラメータ $w_i$ はM個用いられているが,エビデンス近似の枠組みではこのうちデータによって有効なパラメータ数が $\gamma$ に制限され,残りの $M - \gamma$ 個のパラメータの値は事前分布の値,すなわち0に引き寄せられるのである.このとき分散の推定結果( $\beta$ )の割り算において最尤推定の $N-1$ の代わりに $N - \gamma$ を用いられるので,最尤推定による分散の過小評価を抑えることもできる.
図(3.16),図(3.17)においては,9個のガウス基底関数を用いて三角関数のデータをフィッティングした際の結果を示している.図(3.17)においては,有効パラメーター数 $\gamma$ を増やすと0より大きな値をとる $w_i$ の個数が増えていく(だいたい合計が $\gamma$ と等しい)ことが分かる.
$N \gg M$ の場合,$(\beta \Phi{^{\text{T}}}\Phi)\boldsymbol{u}_i = \lambda_i \boldsymbol{u}_i$ において計画行列 $\Phi^{\text{T}}\Phi$ も大きな値をとるので,固有値 $\lambda_i$ も大きな値をとる.よって $\gamma \approx M$ となる.これはデータ数を増やせば増やすほど高次の基底関数を用いても過学習は起きず,それに対応する重みパラメーターも有効となるという現象を示している.このとき
$$\begin{align*} \alpha &= \dfrac{M}{2E_W (\boldsymbol{m}_N)} \\ \beta &= \dfrac{N}{2E_D (\boldsymbol{m}_N)} \end{align*}$$
である.