ガウス過程回帰など
双対表現
観測値が $t_n \sim \mathcal{N}(\boldsymbol{w}^{\text{T}}\boldsymbol{\phi}(x_n),\beta^{(-1)})$ に従うとして以下のように正則化項付きの二乗和誤差を考える.
$$\begin{align*} J(\boldsymbol{w})=\dfrac{1}{2} \sum_{n=1}^{N}{\boldsymbol{w}^{\mathrm{T}} \boldsymbol{\phi}(\boldsymbol{x}_{n})-t_{n}}^{2}+\dfrac{\lambda}{2} \boldsymbol{w}^{\mathrm{T}} \boldsymbol{w} \end{align*}$$
Jの $\boldsymbol{w}$ についての勾配を0とすると
$$\begin{align*} \boldsymbol{w}=-\dfrac{1}{\lambda} \sum_{n=1}^{N}\boldsymbol{w}^{\mathrm{T}} \phi (\boldsymbol{x}_{n})-t_{n} \phi (\boldsymbol{x}_{n})=\sum_{n=1}^{N} a_{n} \phi (\boldsymbol{x}_{n})=\boldsymbol{\Phi}^{\mathrm{T}} \boldsymbol{a} \end{align*}$$
ここで $\Phi$ はn行目が $\boldsymbol{\phi}(x_n)$ で与えられる計画行列である.逆に $\boldsymbol{w} = \boldsymbol{\Phi}^{\text{T}} \boldsymbol{a}$ を用いるとJ(w)は
$$\begin{align*} J(\mathrm{a})=\frac{1}{2} \mathrm{a}^{\mathrm{T}} \Phi \Phi^{\mathrm{T}} \Phi \Phi^{\mathrm{T}} \mathrm{a}-\mathrm{a}^{\mathrm{T}} \Phi \Phi^{\mathrm{T}} \mathrm{t}+\frac{1}{2} \boldsymbol{t}^{\mathrm{T}} \mathrm{t}+\frac{\lambda}{2} \mathrm{a}^{\mathrm{T}} \Phi \Phi^{\mathrm{T}} \mathrm{a} \end{align*}$$
と表せる.さらにグラム行列を $\boldsymbol{K} = \boldsymbol{\Phi}^{\text{T}} \boldsymbol{\Phi}$ で定義すると
$$\begin{align*} J(\boldsymbol{a})=\frac{1}{2} \boldsymbol{a}^{\mathrm{T}} K K \boldsymbol{a}-\boldsymbol{a}^{T} K t+\frac{1}{2} t^{T} t+\frac{\lambda}{2} \boldsymbol{a}^{T} K \boldsymbol{a} \end{align*}$$
これを $\boldsymbol{a}$ について微分して解くと
$$\begin{align*} \mathrm{a}=(\boldsymbol{K}+\lambda \boldsymbol{I}_{N})^{-1} \boldsymbol{t} \end{align*}$$
を得る.これを $y(\boldsymbol{x}) = \boldsymbol{w}^{\text{T}} \boldsymbol{\phi}(\boldsymbol{x})$ に代入すると
$$\begin{align*} y(\boldsymbol{x}) = \boldsymbol{k}(\boldsymbol{x})^{\mathrm{T}}(\boldsymbol{K}+\lambda \boldsymbol{I}_{N})^{-1} \boldsymbol{t} \end{align*}$$
が得られる.ここで $\boldsymbol{k}(\boldsymbol{x})$ は $k_n(\boldsymbol{x}) = k(\boldsymbol{x}_n, \boldsymbol{x})$ を要素とするベクトルである.
カーネル関数
$k(\boldsymbol{x}, \boldsymbol{x}^{\prime})$ は有限次元のベクトル $\boldsymbol{\phi}(\boldsymbol{x})$ の内積として表されるものでも良いし,単なる関数を用いると無限次元のベクトルの内積として表現できることもある.
例えば $k(\boldsymbol{x}, \boldsymbol{z}) = (\boldsymbol{x}^{\text{T}} \boldsymbol{z})^2$ は有限次元の特徴ベクトル
$$\begin{align*} \phi(\boldsymbol{x})=(x_{1}^{2}, \sqrt{2} x_{1} x_{2}, x_{2}^{2})^{\mathrm{T}} \end{align*}$$
を用いて $\boldsymbol{\phi}(\boldsymbol{x})^{\mathrm{T}} \boldsymbol{\phi}(\boldsymbol{z})$ と表せる.また以下のガウスカーネル
$$\begin{align*} k(\boldsymbol{x}, \boldsymbol{x}^{\prime})=\exp (-|\boldsymbol{x}-\boldsymbol{x}^{\prime}|^{2} / 2 \sigma^{2}) \end{align*}$$
も有名である.これは無限次元のベクトルの内積と解釈できる.
RBFネットワーク
入力 $\{\boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{N}\}$ と出力 $\{t_{1}, \ldots, t_{N}\}$ に対してデータ点回りで以下のように補完を行う.
$$\begin{align*} f(\boldsymbol{x})=\sum_{n=1}^{N} w_{n} h(|\boldsymbol{x}-\boldsymbol{x}_{n}|) \end{align*}$$
これは訓練データを完全に再現することができるが,出力にノイズが与えられている場合には過学習を引き起こしてしまう.
Nadaraya-Watsonモデル
次に入力 $\boldsymbol{x}$ に雑音 $\boldsymbol{\xi} \sim \nu(\boldsymbol{\xi})$ が加えられて出力 $t_n = y(\boldsymbol{x} + \boldsymbol{\xi})$ が得られるとする.そして訓練集合を $(x_n, t_n) (i = 1, \ldots ,N$ とする.
このとき予測値 $y(\boldsymbol{x})$ は以下のようにして与えられる. $$\begin{align*} y(\boldsymbol{x})=\sum_{n=1}^{N} t_{n} h(\boldsymbol{x}-\boldsymbol{x}_{n}) \end{align*}$$
ここで
$$\begin{align*} h(\boldsymbol{x}-\boldsymbol{x}_{n})=\frac{\nu (\boldsymbol{x}-\boldsymbol{x}_{n})}{\sum_{n=1}^{N} \nu (\boldsymbol{x}-\boldsymbol{x}_{n})} \end{align*}$$
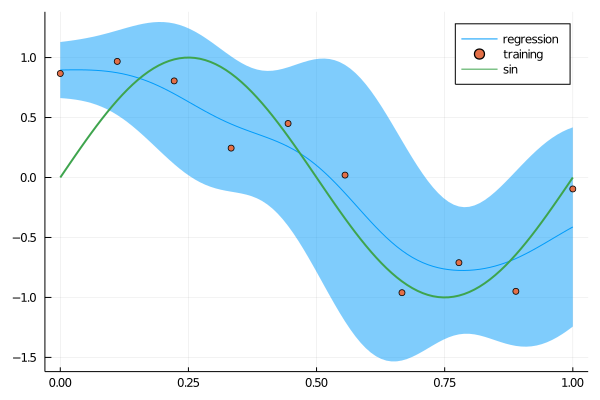
である.下の図は1次元の入力 $x$ に対して $\mathcal{N}(0, \sigma^2)$ に従う雑音が加えられ $y(x) = sin(2 \pi x)$ により生成したデータに対してNadaraya-Watsonモデルを適用した結果である.ここで分散は
$$\begin{align*} \mathrm{var}(t \mid x) &= \mathbb{E}(t \mid x)^2 - ( \mathbb{E}(t \mid x))^2 \\ &= \sum_{n} h_n(t_n2 + \sigma^2) - \left( \sum_n h_n t_n \right) \end{align*}$$
で与えられ,図では $\pm 2\sigma$ 区間がリボンで示されている.
ガウス過程
$y(\boldsymbol{x})=\boldsymbol{w}^{\mathrm{T}} \boldsymbol{\phi}(\boldsymbol{x})$ において $\boldsymbol{w}$ の事前分布として以下の分布を考える.
$$\begin{align*} p(\boldsymbol{w})=\mathcal{N} (\boldsymbol{w} \mid \boldsymbol{0}, \alpha^{-1} \boldsymbol{I}) \end{align*}$$
$\boldsymbol{w}$ は確率変数であるから, $y(\boldsymbol{x})$ もガウス分布に従う確率変数である. $\boldsymbol{\Phi}$ を各行が $\boldsymbol{\phi}^{\text{T}}(\boldsymbol{x})$ である計画行列とし,
$$\begin{align*} \boldsymbol{y} = \boldsymbol{\Phi w} \end{align*}$$
とすると, $\boldsymbol{y}$ もガウス分布に従う.そして
$$\begin{align*} \mathbb{E}[\boldsymbol{y}] &= 0 \\ \mathrm{cov}[\boldsymbol{y}] &= \mathbb{E}[\boldsymbol{y}\boldsymbol{y}^{\text{T}}] = \boldsymbol{\Phi} \mathbb{E}[\boldsymbol{ww}^{\text{T}}] \boldsymbol{\Phi}^{\text{T}} = \frac{1}{\alpha} \boldsymbol{\Phi \Phi}^{\text{T}} = K \end{align*}$$
である.
ガウス過程回帰
観測される目標変数 $t_n$ にはガウス分布に従うノイズが含まれると仮定する.
$$\begin{align*} p (t_{n} \mid y_{n})=\mathcal{N}(t_{n} \mid y_{n}, \beta^{-1}) \end{align*}$$
そして目標値 $\boldsymbol{t} = (t_1, \ldots , t_N)^{\text{T}}$ の同時分布も以下の等方的なガウス分布に従う.
$$\begin{align*} p(\boldsymbol{t} \mid \boldsymbol{y})=\mathcal{N}(\boldsymbol{t} \mid \boldsymbol{y}, \beta^{-1} \mathrm{I}_{N}) \end{align*}$$
入力値で条件づけられた $p(\boldsymbol{y})=\mathcal{N}(\boldsymbol{y} \mid \boldsymbol{0}, \boldsymbol{K})$ を用いて
$$\begin{align*} p(\boldsymbol{t})&=\int p(\boldsymbol{t} \mid \boldsymbol{y}) p(\boldsymbol{y}) \mathrm{d} \boldsymbol{y}=\mathcal{N}(\boldsymbol{t} \mid \boldsymbol{0}, \boldsymbol{C}) \\ \boldsymbol{C}_N &= K + \beta^{(-1)}\boldsymbol{I}_N \end{align*}$$
となる.
予測分布
$\boldsymbol{t}_{N+1} \sim \mathcal{N}(0, \boldsymbol{C}_{N+1})$ において
$$\begin{align*} \begin{pmatrix} \boldsymbol{C}_N & \boldsymbol{k} \\ \boldsymbol{k}^{\text{T}} & c \end{pmatrix} \end{align*}$$
と分割できる.ここで$c = k(\boldsymbol{x}_{N+1}, \boldsymbol{x}_{N+1}) + \beta^{-1}$)
$$\begin{align*} c &= k(\boldsymbol{x}_{N+1}, \boldsymbol{x}_{N+1}) + \beta^{-1} \\ \boldsymbol{k}(\boldsymbol{x}_{N+1}) &= [k(\boldsymbol{x}_{N+1}, \boldsymbol{x}_1), \ldots , k(\boldsymbol{x}_{N+1}, \boldsymbol{x}_N)] \end{align*}$$
$\boldsymbol{t}_N$ が観測値として与えられると条件付き分布 $p(t_{N+1} \mid \boldsymbol{t})$ は以下の平均と分散を持つ.
$$\begin{align*} m(\boldsymbol{x}_{N+1}) &= \boldsymbol{k}^{\mathrm{T}} \boldsymbol{C}_{N}^{-1} \boldsymbol{t} \\ \sigma^{2}(\boldsymbol{x}_{N+1}) &=c-\boldsymbol{k}^{\mathrm{T}} \boldsymbol{C}_{N}^{-1} \boldsymbol{k} \end{align*}$$
これらが $\boldsymbol{x}_{N+1}$ の関数になっていることは重要な点である.この平均値は
$$\begin{align*} m (\boldsymbol{x}_{N+1})=\sum_{n=1}^{N} (\boldsymbol{Ct})_{n} k(\boldsymbol{x}_{n}, \boldsymbol{x}_{N+1}) \end{align*}$$
とも書けるからRFBと類似している.
ハイパーパラメータの学習
ここでいうハイパーパラメーターとは,例えばカーネル関数 $k(\boldsymbol{x},\boldsymbol{x}’) = a\exp(-b(\boldsymbol{x} - \boldsymbol{x}’)^2)$ における $\boldsymbol{\theta} = (a, b)^{\text{T}}$ のことである.これはエビデンス関数 $p(t \mid \boldsymbol{\theta})$を最大化することで行われる.対数エビデンス関数は
$$\begin{align*} \ln p(\boldsymbol{t} \mid \theta) = -\frac{1}{2}\ln |\boldsymbol{C}_N| - \frac{1}{2}\boldsymbol{t}^{\text{T}} \boldsymbol{C}_N^{-1}\boldsymbol{t} - \frac{N}{2}\ln(2\pi) \end{align*}$$
であり,これを微分すると
$$\begin{align*} \frac{\partial}{\partial \theta_{i}} \ln p(\boldsymbol{t} \mid \theta)=-\frac{1}{2} \mathrm{Tr}\left(\boldsymbol{C}_{N}^{-1} \frac{\partial \boldsymbol{C}_{N}}{\partial \theta_{i}}\right)+\frac{1}{2} \boldsymbol{t}^{\mathrm{T}} \boldsymbol{C}_{N}^{-1} \frac{\partial \boldsymbol{C}_{N}}{\partial \theta_{i}} \boldsymbol{C}_{N}^{-1} \boldsymbol{t} \end{align*}$$
が得られる.
関連度自動決定(ARD)
以下のように用意した変数 $(x_1, x_2, x_3)$ と目標変数 $t$ を考える.
$$\begin{align*} x_1 &\sim \mathcal{N}(0) \\ x_2 &= x_1 + \mathcal{N}(0) \\ x_3 &\sim \mathcal{N}(0) \\ t &= \sin(2 \pi x_1) + \mathcal{N}(0) \end{align*}$$
この中で $t$ を予測するうえで $x_1$ は最も相関があり,その次に $x_2$ , $x_3$ は全く相関がない.ここで $\boldsymbol{x} = (x_1, x_2, x_3)$ を入力,出力を $t$ としてカーネル関数を
$$\begin{align*} k(\boldsymbol{x}, \boldsymbol{x}^{\prime}) = \theta_0 \exp \left( -\frac{1}{2} \sum_{i=1}^{3} \eta_i (x_i - x_i^{\prime})^2 \right) \end{align*}$$
としてハイパーパラメーター $(\theta_0, \eta_0, \eta_1, \eta_2)$ を学習させると教科書の図6.10のように $\eta_3$ は非常に小さな値に収束する.このように予測分布に対して寄与しない変数を検出することができるため,スパースなモデルを得られる.