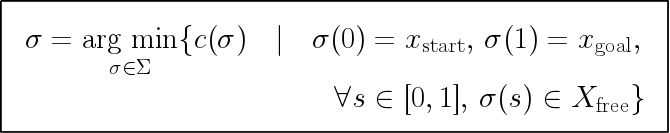Informed RRT*: Optimal Sampling-based Path Planning via Direct Sampling of an Admissible Ellipsoidal Heuristic¶

本ノートはInformed RRT Star(InformedRRTStar*が提唱された論文の読書ノートである．RRT-Starにおいて最初の解が得られた際に，サンプリング範囲をその一時的な解の周辺の楕円に絞ることで，最適解への漸近をより早めることができるというもの．楕円を使うあたりに，著者らの頭の良さを感じる．

Date: 3/20

Author:	Jonathan D. Gammell, Siddhartha S. Srinivasa, and Timothy D. Barfoot
Year:	2014
Accepted:	arXiv:
Detail:	arXiv:1404.2334v3 [cs.RO] 28 Nov

Abstract¶

Rapidly-exploring random trees(RRTs)はsingle-queryの経路計画問題に対しては効率的に解を求められるためポピュラーである(学術的に，多分)．Optimal RRTs(RRT*)はRRTを最短解を求める問題へと拡張する．しかし初期状態から探索木における 一つ一つの全てのノードへの 最短解を漸近的に求める．この振る舞いは非効率的なだけでなく，sigle-queryという元々のRRTの性質と一貫性がない(single-queryに対してのみ最短経路を求めればよいのに，無駄なことをしている)．

経路を短くしようという問題においては，解をrefineしうる状態の部分集合は超楕円として表すことができる．もし探索空間が比較的大きいか次元が高い場合，この超楕円から直接サンプリングを行わない限り得られた解がさらに最短解へと収束する確率は0へと収束することを示す．

このようにしてサンプリングを行うことの利点を活用して， Informed RRT* なる新しいアルゴリズムを提案する．この手法はRRT*のprobabilistic complentenessとasymptotic optimalityを保持しているが，RRT* に比べ収束率と最終的な解のqualityが改善されている．このアルゴリズムは他のより優れたpath-planningのアルゴリズムにも拡張できるようRRT* を簡潔に拡張している．このアルゴリズムはシミュレーションにより，状態空間の次元やplanning problemの範囲によらずRRT* を，収束率や最終解のコスト，diffucut passagesを探索する能力において上回ることを示す．

Introductions¶

motion-planningは，グリッドベースの手法か，インクリメンタルサーチを用いるサンプリングベースの手法により，まず初めに状態空間を離散化してから行われるのが普通である．A* (P. E. Hart, N. J. Nilsson, and B. Raphael (1968))に代表されるグリッドベースの手法は resolution complete や resolution optimal と言われる．これらの手法はもし解が存在するのならば解像度や離散化の粒度に制限されるものの最短解を得られることが保証されている．これらのグリッドベースの手法は探索空間の次元が高くなると現実的でない(do not scale well with problem size)．

Rapidly-explopring random trees(S. M. Lavalle and J. J. Kuffner Jr (2001))やProbabilistic Roadmap Method(L.E.Kavraki, P. SVestka, J.-C.Latombe, and M. H. Overemars (1996))，Expansive Space Trees(D. Hsu, R. Kindel, J. -C. Latombe, and S. Rock (2002))といった確率的に探索を行う手法は，サンプリングを用いることで探索空間の離散化を必要としない．それにより問題のサイズによくスケールしkinodynamic constraintsを直接考慮することができる．その代わりにcompletenessの保証が弱い．RRTとその亜種は probabilistic complete である，すなわちもし解が存在しているのであれば探索回数を増やせば増やすほど，解が見つかる確率が1に近づく(こう書くと当たり前にも聞こえる)．最近までこれらのサンプリングベースの手法は解の optimality については言及されて来なかった． Urmson and Simmons(2003)らはサンプリングをバイアスするためにヒューリスティックを用いることでRRTの解を改善することができることを示したがその改善効果をきちんとは定量化してはいない．Ferguson and Stenz(2006)は解となる経路の長さがその改善効果に限度をかけていることに気づき，一連のより小さいplanningを解く，逐次的anytime RRTを提唱した(それにしてもanytimeの意味が未だに分からない)．Karaman and Frazzoli(2011)はRRTは確率1でsuboptimalな解を返すことを示し，新たなクラスのoptimal plannerを提唱した．彼らはそれらをRRT*，PRM*と名付けた．これらのアルゴリズムは asymptotically optimal ，すなわちイテレーションが無限大に近づくほど最適(最短)解を求める確率が1に近づくことが示されている．

RRTがasymptotically optimalでない理由は，各段階での状態グラフが，それから先のグラフの伸長にバイアスを与えるからである(その標本が発散してしまう感じ．最適解へと収束せず離れてしまう)．RRT* ではグラフをインクリメンタルに再接続を行うことでこれを克服している(フィードバックに近いかもしれない)．新しい状態は探索木に単純に加えられるだけでなく，周辺の既存のノードの代わりの親の候補となる．大域的に一様分布によりサンプリングを行うと，このアルゴリズムは 初期状態から，対象とする領域全体に分布する全てのサンプルードに対して，漸近的に最短経路を求めることで single-queryの最短経路問題を解くことになる．これはRRT のsingle-queryの性質と相性が悪く，高次元においては計算コストが大きい．

この論文では \(\mathbb{R}^{n}\) における経路を最小化するのに特化したoptimal planning problemを対象とする．そのような問題において現在の解を改善するための必要条件は，対象領域の超楕円の部分集合からノードを加えることである．我々は，一様分布によりその部分集合からノードがサンプルされる確率は，対象領域が大きくなったり解が理論的な最小値に近づいたりするにつれて，任意に小さくなることを示す．そしてその超楕円から直接サンプリングを行う．また障害物が存在しないという厳しい仮定の下で，そのサンプリングを行うことで得られる解は最短解へと一次収束することも示す．

Informed RRT* は解が見つかるまではRRT* と同様の振る舞いを示す．そして一旦その解が見つかった後はadmisssible heuristic により定義される部分集合のみからサンプリングを行う．この部分集合を定めるのにはチューニングは必要なく，explorationとexploitationを陰に両立する．ヒューリスティックを用いることで常に探索の効率が良くなるわけでないが，もしヒューリスティックが何ら情報をもたらさない場合(例えば全空間を探索するようなヒューリスティック，全空間を一様分布で探索するからベイズにおける無情報信念といったところか)Informed RRT* は RRT* と全く同様に振る舞う．

focused searchを行うおかげでこの手法は探索空間の次元や対象領域の大きさにそれほど依存しない(収束率がってことね．)．またトポロジーの異なる，より最短に近い経路をより素早く探索することができる．また障害物が存在しない場合マシンゼロの精度で有限時間内に最短解を見つけることができる．

この論文は以下のような構成になっている．第2章においてfocused optimal planningの正式な定義と既存の手法のreviewを行う．第3章において解を改善しうる部分集合を閉じた形で表し，RRT* スタイルのアルゴリズムへのimplicationを解析する．第4章においてInforme RRT* の解説を行い，第5章においてシミュレーションとRRT* との比較を行う．

Background¶

Problem Definition¶

ここではKaraman and Frazolli(2011)に従いoptimal planning problemを定義する． \(X \in \mathbb{R}^{n}\) をdomain of planning problem, \(X_{obs} \in X\) を障害物の存在する領域， \(X_{free} = X - X_{obs}\) をpermissible statesの部分集合とする． \(x_{start} \in X_{free}\) を初期の点， \(x_{goal} \in X_{free}\) を終点とする．この2点を接続する経路は \(\sigma: [0, 1] \mapsto X\) である．optimal path planningとはコスト関数 \(c: \Sigma \mapsto \mathbb{R}_{>0}\) が与えられた時に以下の条件を満たす \(\sigma{*}\) を求めることである．

\(f(x)\) を経路のコストとする．すると現在の解を改善しうる部分集合 \(X_{f}\) は以下のように表される．

\begin{align*} X_{f} = \{ x \in X \, | \, f(x) < c_{best} \} \end{align*}

RRT* において収束率を上げることは，ノードがこの領域からサンプリングされるようにすることである．

この関数は実際は分からないので(多分cost-to-goなんだろうな)代わりにヒューリスティック関数 \(\hat{f}\) が使われる．このヒューリスティック関数は，もし経路の 本当のコストを過大評価しないならば admissibleであると言われる．すなわち

\begin{align*} \forall x \in X, \hat{f}(x) < f(x) \end{align*}

であるということ．もし真のコストを過小評価するとどうなるか．そのヒューリスティックは 実際は真の解のコストより大きくなっている経路を，勘違いして真の解より最適であると みなしてしまうため，探索があらぬ方向へ向かってしまうということだろう．そのため， \(X_{f}\) の推定値である \(X_{\hat{f}}\) は \(X_{\hat{f}} \supset X_{f}\) である(もしこれが逆で \(X_{\hat{f}} \subset X_{f}\) だったら，真の経路を外す可能性があるので)．

Prior Work¶

ここから1ページ半，従来法が続く．さすがよく調べている．

RRT/RRT* の(サンプリングをfocusする)従来手法では

sample biasing
heursitic-based sample rejection
heuristic-based graph pruning
iterative search

が知られている．

Sample Biasing¶

sample biasingでは \(X\) からのサンプリングの確率分布にバイアスをかけることでノードが \(X_{f}\) からよりサンプリングされるようにする．しかしこれは解を改善しえない \(X_{f}\) の外からもサンプリングを続ける．また探索範囲において一様でない確率分布になるためRRT* の重要な前提を破っている．

Heuristic-based Sampling

論文を読まないと分からないが，おそらくヒューリスティックな確率分布を用いて各状態の尤度的なものを評価して重み付けすることで \(X_{f}\) からサンプリングされやすくなるようにしている．Urmson and Simmons(2003)ではヒューリスティックにより評価したコストの逆数に比例する確率でノードが選ばれる陽にするHeuristically guided RRTを提唱している(意外と子供だましな発想)．RRTより良い結果を得ることができているが，基本的にRRTとその亜種はsuboptimalな解しか得られない．

Keisel et al. (2012)では2段階に分けて問題を解くことでRRT* にヒューリスティックを導入している．初めに粗い離散化をした上で問題を解き，各々のブロックのコストのヒューリスティックを求めている(cost-to-goの近似値，多分)．それからRRT* は，離散化したブロックからのサンプリング，さらにそのブロック内でのサンプリングを行う．ブロックのサンプリングでは，離散化の段階での解(粗いグリッドでの経路)が最も選ばれやすいようバイアスがかけられる．一方各々のブロック内では一様分布である．

Path Biasing

path-biased samplingでは現在の解の周辺でサンプリングを行うことで \(X_{f}\) からのサンプルを増やそうとする．これは，現在の解は最適解とホモトピーが同じか少数の障害物を間に挟んでいる程度という仮定を行っている．この仮定は常には正しくないため，局所極小解を避けるためにまだ大域的なサンプリングを続けねばならない．Alterovitz et.al (2011)はPRMを構築するのにpath-biasingを用いている．一旦解が求まったら，それからは新しいノードをサンプルするか，現在の解のノードを選んでrefineを行う．

Akgun and Stilman(2011)はdual version RRT*(bidirectionalのこと?)においてpath-biasingを用いている．ここでは一旦解が求まった後，ユーザーが指定した割合で現在の解のrefinementを行う．その際は解に含まれるノードをランダムに選んで，そのボロノイ領域からサンプリングを行う．これはホモトピーの異なる解を探索する代わりに現在の解を改善する確率をあげることになる．

Nasier et.al(2013)においてはRRT* -Smartと名付けられたアルゴリズにおいてpath-biasingとsmoothingが組み合わされている．解が一旦求まったら，その解にsmoothingを適用してノードの数を最小限に減らす(それらを将来のbiasingに用いることはしない)．これはplannerをpath-smoothingの分複雑にするのと，まだ局所解を避けるためにglobalなサンプリングを必要とする．path-smoothingにより現在の解のコストは減らすことができるが，ノードを削ることにより将来のbiasingによりホモトピーの異なる経路を探索する確率を減らすことに繋がる．

Heuristic-based Sampling Rejection¶

Heuristic-based sample rejectionは \(X\) において棄却サンプリングを行うことで \(X_{f}\) からのサンプリングを増やそうとし，結果 \(X_{\hat{f}}\) からのサンプリングを増やす．larger distributionからサンプルされたノードはヒューリスティックな評価値により保持/棄却するかが決められる．これは一回の繰り返しでは計算負荷は小さいが，the number of iterations necessary to find a single state in \(X_{\hat{f}}\) is proportional to its size relative to the sampling domain. This becomes nontrivial as the solution approaches the theoretical minimum or the planning domain grows.

Graph Pruning¶

Graph Pruningにおいては，グラフを \(X_{\hat{f}}\) へと制限するためにヒューリスティック関数を用いることで \(X_{f}\) からのサンプリングを増やす．現在の解のコストよりヒューリスティックのコストが大きいノードは探索グラフから周期的に枝刈りされる一方大域的なサンプリングも続けられる．RRTは空間をカバーしようとする傾向があるので(space-filling nature) \(X_{\hat{f}}\) の境界へ向かって枝刈りされた探索木の伸長にバイアスをかける．この部分集合がカバーされた後は \(X_{\hat{f}}\) からの状態のみが新たにグラフへと加えられる．このようにしてgreedlyに目標とする部分集合をカバーした後，枝刈りを行うのは棄却サンプリングを行うことになる．RRTへと新たにを加える際，最近傍探索を要するので枝刈りは単純な棄却サンプリングに比べて計算コストが高い．また同様のprobabilistic limitationsに直面する．

Karamn et. al(2011)らは実行中に解を改善するanytimeなRRTにおいて枝刈りを利用している．そこでは現在の解を改善するために，各ノードは現在のコストにプラスとしてゴールまでのヒューリスティックなコストを加えて評価され，現在の解を改善する見込みのないノードは枝刈りされる．RRT* はノードの(真の)コストに漸近的に 上から 近づくものなので，このヒューリスティックはinadmissibleである(何か過大評価してるっけ...?)．これは特に初期において探索木が粗い時にノードのコストを過大評価し，誤って(本当は真の経路に含まれるはずの)ノードを削除しかねない．

Anytime RRT*¶

Ferguson and Stentz(2006)では，解が求まると，それを改善しうる部分集合も限定されることに気付いている．彼らの提唱したiterative RRT(Anytime RRT, Anytimeってそういうことね)では，一つ前の段階での解から定義されるplanning domain において一連の独立したplanning problemを解く(再帰的に)．その論文において彼らはplanning domainを楕円として表現していたが，どのようにしてサンプルを生成するかについては議論していない．planning domainを制限することでRRTは一つ前よりより良い解を見つけようとするが， \(X_{\hat{f}}\) においてすでに見つかった状態をdiscardしないといけない(だからどうなる?)．

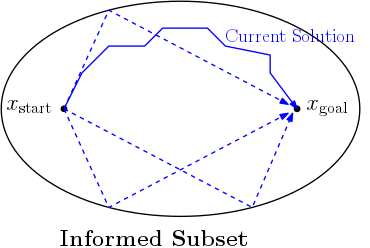
本論文において提案されるアルゴリズムは \(X_{\hat{f}}\) を明示的に計算しそこから直接サンプリングを行う(新規性はおそらくこの2つ)．path-biasingとは異なりこの手法は最適経路のホモトピー類について仮定をおかず，またheuristic-baisingと異なり解を改善し得ないノードは探索しない．RRT* 基づいているため探索途中で見つかった \(X_{\hat{f}}\) に属するノードは保持し続ける． \(X_{\hat{f}}\) から直接サンプリングを行うことで \(X\) との相対的なサイズによらず，解を改善しうるノードだけをサンプルする．またそれによりsample-rejectionやgraph-pruningとも異なり理論値と比べて現在の解が相対的に離れていてもうまく動く．

Analysis of the Ellipsoidal Informed Subset¶

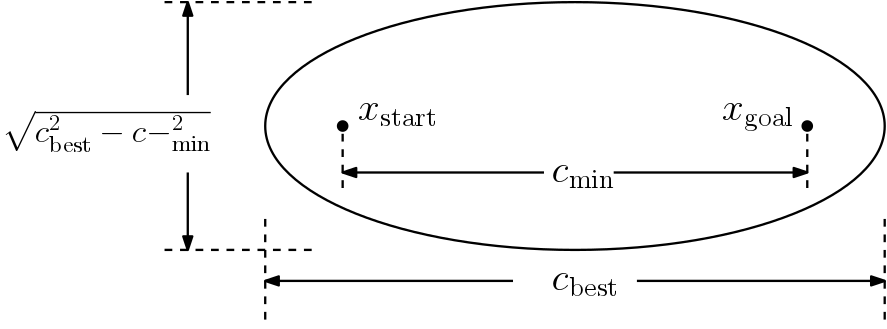
正の値をとるコスト関数が与えられた時， \(x_{start}\) から \(x_{goal}\) へ \(x\) を経由する最短経路のコスト \(f(x)\) は \(x_{start}\) から \(x\) へのコスト \(g(x)\) と \(x\) から \(x_{goal}\) へのコスト \(h(x)\) の和に等しい．RRT* ベースのアルゴリズムは 上から (どんどん短くなっていく)最短経路へと近づくので，admissibleなヒューリスティック関数 \(X_{\hat{f}}\) はこれらの2項を両方満たさねばならない．つまり \(g(x)\) と \(h(x)\) が両方共 \(\hat{g}(x)\) と \(\hat{h}(x)\) のadmissibleな推定値になっていなければならない． \(\mathbb{R}^{n}\) において経路を最小化しよういう問題においてはユークリッド距離がadmissbleなコスト関数となる．現在の解を改善しうるノードの部分集合(== informed subset) \(X_{\hat{f}} \supset X_{f}\) は現在の解のコスト \(c_{best}\) を用いて以下のように表される．

\begin{align*} X_{\hat{f}} = \{ x \in X \quad \mathrm{s.t.} \quad |x_{start} - x|_{2} + |x - x_{goal}|_{2} \leq c_{best}\} \end{align*}

これはn次元における超楕円の一般的な定式である．ここで \(x_{start}\) ， \(x_{goal}\) はこの超楕円の焦点であり，長軸は \(c_{best}\) ，短軸は \(\sqrt{c_best^{2} - c_{min}^{2}}\) である．

\(X_{\hat{f}}\) を包含する部分集合 \(X_{s}\) から一様分布を用いて \(X_{\hat{f}}\) から \(x_{i+1}\) が得られて解が改善される確率は

\begin{align*} P(c^{i+1}_{best} < c^{i}_{best}) &\leq P(x^{i+1} \in X_{f}) \\ &\leq P(x^{i+1} \in X_{\hat{f}}) = \frac{\lambda(X_{\hat{f}})}{\lambda(X_{s})} \end{align*}

n次元における超楕円の体積を計算することでこの確率は以下のように評価される．

\begin{align*} P(c_{best}^{i+1} < c_{best}^{i}) \leq \dfrac{c_{best}^{i}(c_{best}^{i} - c_{min}^{2})^{n(n-1)/2} \xi_{n}}{2^{n}\lambda (X_{s})} \end{align*}

ここで \(\xi_{n}\) はn次元における球の体積である．

Remark 1(棄却サンプリング)¶

上の式から一様分布を用いて解を改善することのできる確率は， \(X_{s}\) が比較的大きい場合や現在の解のコストが理論的な下限に近づくにつれて0に収束する．

解説¶

つまり \(c_{best}^{i}\) が \(c_{min}\) に近づくか，または \(\lambda (X_{s})\) が大きくなると確率が0に収束する．始点と終点を結ぶ「ヒモ」は連続的に伸びたり縮んだりするが，現在の解より小さい経路(直線距離で)は楕円を描く．

Remark 2(Rectangular rejection sampling)¶

もしここで \(X_{s}\) が図の楕円を囲む長方形であれば(辺の長さがそれぞれ長軸と短軸の長さに等しい)一様分布により \(X_{s}\) からのサンプルが \(X_{\hat{f}}\) に入る確率は \(\xi_{n} / 2^{n}\) である．これはnが増えるにつれて急速に減少するため(球面集中現象!!)棄却サンプリングにより解が改善される確率はかなり小さい．

Theorem 1(Obstacle-free linear convergence)¶

もし障害物が存在しない場合，Informed Subsetから一様的にサンプリングを行うことで \(c_{best}\) は理論的な最小値へと収束することを示す．

証明¶

状態 \(x\) のヒューリスティックな評価値は \(x_{start}\) と \(x_{goal}\) を焦点にもち \(x\) を通る超楕円のtransverse diamiter(横半径)に等しい．一様分布を使うとその期待値は

\begin{align*} E[\hat{f}(x)] = \dfrac{nc_{best}^{2} + c_{min}^{2}}{(n+1)c_{best}} \end{align*}

である．

ここではRRT* のasymptotic optimalityに関する証明がなされている論文と同様に，RRT* のrewiringを行う際の探索半径のスケーリングパラメータ \(R\) は十分大きいと仮定する．改善された経路の長さの期待値 \(c_{best}^{i}\) はtransverse diamiterが \(c_{best}^{i-1}\) である超楕円からのサンプルのヒューリスティックの評価値である．すなわち

\begin{align*} E[c_{best}^{i}] = E[\hat{f}(x^{i})] \end{align*}

2つ上の式から解の収束率は以下のような次元nにのみ依存するパラメータに従って線形に収束する．

\begin{align*} \mu = \left.\dfrac{\partial E[c_{best}^{i}]}{\partial c_{best}^{i-1}}\right|_{c_{best}^{i-1} = c_{min}} = \dfrac{n-1}{n+1} \end{align*}

障害物が存在しないという仮定はimpracticalではあるがこのような解析はinformed subsetからサンプリングを行うことの有効性を示している．

Direct Sampling of an Ellipsoidal Heuristic¶

ようやくここまで読んで気付いたのだが，今まで出てきた \(x_{ellipse} \sim \mathcal{U}(X_{ellipse})\) の \(\mathcal{U}\) って一様分布のUniformだったのか．とにかくこの領域からのサンプリングはn次元の単位球における一様分布を以下のようにアフィン変換することで得られる．

\begin{align*} x_{ellipse} = Lx_{ball} + x_{center} \end{align*}

ここで \(x_{center}\) は2つの焦点の中心である．また行列 \(L\) は以下のようにして計算される．超楕円は以下のように二次形式により表現されるから

\begin{align*} (x - x_{center})^{T}S(x - x_{center}) \end{align*}

この正定値行列 \(S\) をコレスキー分解した行列が \(L\) である．

\begin{align*} LL^{T} = S \end{align*}

先ほどの図の超楕円は

\begin{align*} S = \mathrm{diag} \{ c_{best}^{2}/4, (c_{best}^{2} - c_{min}^{2})/4, \cdots (c_{best}^{2} - c_{min}^{2})/4 \} \end{align*}

と表されるから

\begin{align*} L = \mathrm{diag} \{ c_{best}/2, \sqrt{c_{best}^{2} - c_{min}^{2}}/2, \cdots \sqrt{c_{best}^{2} - c_{min}^{2}}/2 \} \end{align*}

が得られる．

超楕円における座標軸から(frame)world-frameへの変換は general Wahba problemとして直接解くことができることが知られている．その際の回転行列 \(C\) は以下のように表すことができる．

\begin{align*} C = U \mathrm{diag} \{ 1, ..., 1, \mathrm{det}(U), \mathrm{det}(V) \} V^{T} \end{align*}

ここで行列 \(U\) と \(V\) はある行列 \(M\) を特異値分解した \(U\Sigma V^{T} = M\) なる行列である．行列 \(M\) は以下のようなベクトル \(a\)

\begin{align*} a = (x_{goal} - x_{start}) / |x_{goal} - x_{start}|_{2} \end{align*}

を用いて

\begin{align*} M = a \bf{1}^{T} \end{align*}

と表される．

超楕円で表されるInformed-Subsetから一様に分布するサンプル \(x_{\hat{f}} \sim \mathcal{U}(X_{\hat{f}})\) を得るにはn次元球からの一様分布を以下のように変換すれば良い．

\begin{align*} x_{\hat{f}} = CLx_{ball} + x_{center} \end{align*}

Informed RRT*¶

Informed RRT* のアルゴリズムを下に示す．Informed RRT* は途中まではRRT* と同様に解を探索するが，一旦解が見つかったら解を改善しうる部分集合にサンプリングをフォーカスする．InGoalRegion()において，見つかった解を全て格納し， \(c_{max}\) を更新する．

Discussion¶

Informed RRT* は，ヒューリスティックを用いることでオリジナルのplannig domainの部分集合へとshrinkする．著者らはInformed RRT* においてinitial solutionがなくてもよいよう，Batch Informed Trees(BIT*)を現在開発している．