Randomized Kinodynamic Planning

本ノートは Rapidly Exploring Random Tree (RRT) の Probabilistic Completeness についての証明を含んでいる論文の読書ノートである．KuffnerさんがJSKにいたとき?に書かれたものかもしれない．compeleteness の証明については，RRT-Connect でも触れられている．

Date: 2019/2/2

Author:Steven M. Lavalle, James J.Kuffner, Jr.
Year:2001
Link:http://msl.cs.uiuc.edu/~lavalle/papers/LavKuf01b.pdf
Accepted:The International Journal of Robotics Research

Abstract

この論文はkinodynamic planningに対してrandomized approachをとる最初の論文である．初期のconfigurationと速度から終端のconfigurationと速度へと状態をderiveするような，系のダイナミクスに従いながらもロボットの作業環境における障害物を回避することのできる制御入力を求めることが目的である．

kinodynamic planningは一階の微分方程式による微視的な制約とグローバルな障害物の制約を持つ高次元の状態空間におけるmotion plannningである．basicなpath planningに対してはstate-spaceはconfiguration-spaceと同じ役割を果たす．しかし標準的なpath planningのrandomizedされた手法はstate spaceにおける軌道計画には適用できない(inevitable collisionとかかな)．著者たちは高次元のstate spaceにtailoredされたrandomiedな軌道計画手法を提案した．このアプローチの基本としてはRRTを構築することである:RRTはその他のrandomizedなholonomic planningの手法と同じような利点があり，かつより広いクラスの問題に対して適用できる．

本論文は理論的な解析(probabilistic completenessの証明)を含む．

Introduction

初期のconfiguration(一般化座標のことだろう，多分)だけでなくその一階微分(一般化速度)も境界条件に入れた一般的な，効率的な計画手法が強く求められている．問題は，グローバルな障害物回避の制約とローカルな微分拘束を満たすようなfesibleなオープンループの軌道を求めることである．そのような問題をここではDonald(1993)に従い kinodynamic planning と呼ぶ．非線形制御の文脈では，劣駆動系のkinodynamic planningはnonholonomic planningという用語で総称される．制御理論的な用語では，この研究は慣性項と非凸な制約を受ける非線形な系に対するオープンループの軌道計画である．

ロボティクスにおいてはノミナルな軌道を

  • mobile robots
  • manipulators
  • space robots
  • humanoids

などに対して設計できる．この軌道を参照値としてフィードバックシステムに組み込むこともできる．

ロボティクスにおける古典的なアプローチはbacinなpath planningを解いた後dynamicsを満たし経路に追従するような軌道と制御器を設計することであった．基本的なpath planningの大部分ではkinematicsのみが考慮されており，システムのダイナミクスは全く考慮されていなかった．それはplanningとcontrolがdecoupledされていたため．

純粋にkinematicsな計画器による軌道はトルクや力の制限により実行可能でないこともある．実際のロボットにおいては制御のimprecisionはよくあり，衝突しない経路を保証するためにはシステムのダイナミクスを陽にモデル化する必要があるかもしれない．ロボットのダイナミクスとして典型的なのは，自然法則や可能な制御入力の限界が各configurationにおける可能な速度に制約を課すものである．

  • helicopters
  • airplanes
  • unanchored space robots

など．

kinodyanmicsを考慮しようという試みは

  • Shahar and Hollerbach(1986)，マニピュレータの関節空間をtesellateして動的計画法ベースの探索を用いて探索の次元を低減することで最短時間軌道を求めるもの
  • Donald(1993)，近似的に最適な解軌道を求める動的計画法ベースのアルゴリズム
  • O'Dunlaing(1987)，代数的に軌道を解析的に求めるもの．ただし1質点系の，速度と加速度制約のかかったものしか求められない．
  • Cherif(1999)，all-terrain vehiclesのためのkinodynamic planningに対する動的計画法ベースの探索．
  • Ferbach(1995)，incrementalな変分法(?)により状態空間で探索を行う．
  • Connolly，Grupen，Souccar(1995)，ハミルトニアン形式の力学を用いる．

このように前例はあるが，低次元(どれくらい？)なシステムや特別な簡略が可能なシステムに対してしか存在していない．randomizedな手法はbasicなholonomic planningに対して効率的だがincompleteな計画器である．本論文ではrandomizedなkinodynamic planningの手法を提案する(ここまで言い切るには従来手法の何かを改善しているのだろう)．

Problem Formulation: Path Planning in the State Space

kinodynamic planningは1階の微分拘束を受ける状態空間におけるpath planningとして定義する．姿勢(configuration)は \(q \in \mathcal{C}\) に，状態(state)は \((q, \dot{q}) \in \mathcal{X}\) に属する．

Differential Constraints

非ホロノミック拘束は剛体のロール角の接触やシステムに印加できる入力の形態により発生する．ラグランジアン形式の力学では \(h_{i}(q, \dot{q}, \ddot{q}) = 0\) と表される．状態空間表現ではこれは \(g_{i}(x, \dot{x}) = 0\) for \(i = 1, 2, \cdots, m < 2n\) と表される．つまり 陰関数定理により 入力の存在が暗示される(なにか深い意味がありそう)．つまり

\begin{align*} \dot{x} = f(x, u) \end{align*}

として表される．

Obstacles in the state space

障害物はstaticで，障害物判定は定数時間でできるとする．

path planningだと \(\mathcal{C}_{free}\) は \(\mathcal{C}_{obs}\) を除くだけで良い．では状態空間は \(\dot{q}\) を射影で取り除けば姿勢空間になるから \(x = (q, \dot{q})\) のうち \(q\) が \(\mathcal{C}_{obs}\) に入るものを \(\mathcal{x}_{obst}\) と定義すれば良いのでは？と思うが，momentumによっては衝突してしまうかもしれない．これを inevitable collision といい(ようやく意味が分かった)， \(\mathcal{X}_{ric}\) と表記する． \(\mathcal{X}_{ric}\) は \(\mathcal{C}_{obs}\) を含むから，より広い概念．状態 \(x\) が \(\mathcal{X}_{ric}\) に属するとは，planningに用いられるintervalにおいてどのような制御入力を用いてもcollisionを避けるができないことである．そのため \(\mathcal{X}_{free} = \mathcal{X} - \mathcal{X}_{obst}\) として定義したほうが正確である．

region of inevitable collision は kinodynamic planningの難しさを直感的に教えてくれる．例えばx軸方向に動く質点系の場合，その時の速度と刻み時間をかけた分の距離を-x方向に障害物からinflationすれば良いと思うかも知れない．しかし正確に求めるのは難しいし， \(\mathcal{X} - \mathcal{X}_{ric}\) のトポロジーは \(\mathcal{X} - \mathcal{X}_{ric}\) とはかなり異なるかもしれない．kinematicには衝突しないかもしれないがkinodynamicな場合解が存在しないかもしれない．本論文では \(\mathcal{X} - \mathcal{X}_{obst}\) を用いる．

A Solution Trajectory

省略．

Why does theis problem present unique challenges?

\(\mathcal{X}\) と \(\mathcal{C}\) の違いは次元数における2倍があるかどうかである．次元の呪いをさけるため先に C-space における randmozed path-planningが提案されてきた． \(\mathcal{X}\) における実用的で効率的なplannerに関する研究が欠けている理由としては決定論的に保証された収束率を持つ最適解を得ることに関心が払われているためかもしれない．高次元の問題に対してはこの要求はinfeasibileであり多くの研究者は計画と制御をdecoupleするアプローチを取ってきた．つまり伝統的なmotion planningの問題を解いてからその解の近傍で軌道を最適化するというアプローチである．

randomized kinodynamic planningによるアプローチがとられて来なかった別の理由としてはドリフトの存在によりkinodynamic planningがかなり難しくなるため．randomized holonomic planningの手法を \(\mathcal{X}_{free}\) において \(\dot{x} = f(x, u)\) を満たすよう拡張することを考えよう．人口ポテンシャル場の手法は，ポテンシャルを減少させるような離散時間の制御入力を逐次求めることができるため，この問題に適しているように見える．dynamical systemの大きな問題点は通常ドリフト項を有していることであり，ゴールにおいてオーバーシュートや振動を生じることである．入念に設計されたポテンシャル関数を用いない限りこの手法は(単独では)うまく動かない． \(\mathcal{X}_{ric}\) に容易に入り込んでしまいそうである．kinodynamic planningにおいてヒューリスティック関数を求めるのはかなり難しい．

PRMもkinodynamic planningに適用可能かもしれない．その際にとくに必要になるのはランダムに生成された2つのconfiguration(or state)を接続する局所計画器である．実際この手法は Svestka and Overmars(1995)においてnonholonomic plannnigにsuccessfullyに適用された．この手法がうまく行った大きな理由の一つとしてはReeds-Shepp pathの存在がある．これにより2つのことなるconfigurationを(特定の曲率と円弧と直線の組み合わせで接続するという意味において)optimal pathで接続できる．さらに複雑なシステム(トレーラーなど)に対してはsteering results(Sekhavat et al．1998)を用いてreasonable raodmap plannerを設計することができる．これらの結果により特定のシステムをconfigurationから別のconfigurationへとdriveすることが可能になり，nilpotentizableなdriftlessなシステムに一般的に拡張することができる．しかしこのconnection problemは非線形コントローラを設計するのと同等に難しい．またこのconnectionを全ての組み合わせのconfigurationに対して行わなければならない．

A Planner Based on RRTs

以上の理由により我々はkinodynamic planningに適したrandomized approachを設計するに至った．人口ポテンシャル場のように"drive forward"し，かつPRMのようにquickly and uniformlyに空間を探索したい．

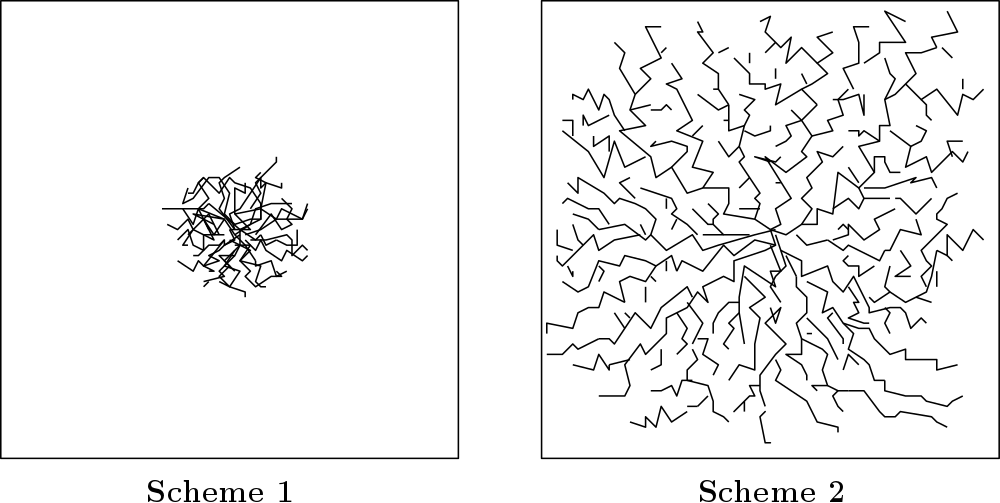
コンセプトを説明するために，初めに2次元の作業空間における1質点のロボットのpath planningを考える．kinodynamic planningに応用することを考えてロボットは \(x_{k+1} = f(x_{k}, u_{k})\) なる離散時間のダイナミクスに従うとする．また制御入力の集合 \(U\) は一定時間において一定距離移動することのできる方角 \(S^{1}\) から選ばれるとする．ここで図のような100x100の領域の中心から探索を始める例を考える．この場合探索方法としては2通り考えることができる．

1つ目は存在している頂点の中から ランダム に \(x_{k}\) を選び，次に制御入力の集合から ランダム に \(u_{k} \in U\) を選びそれを印加してノードを伸ばすことを繰り返して探索木を構築する方法．この方法は一見一様に広がってくれるように思えるが，実は下の左側の図のように，すでに探索している領域へとバイアスがかかってしまい，一様に空間に広がらない．これを克服するため，次のようにしてRRTを構築する．

  1. 初期位置(状態)を加える
  2. 以下を繰り返す
  3. 探索空間からランダムに点を1つ選び，それへの最近傍ノード \(x_{k}\) を求める
  4. サンプルされた点へと向かうような制御入力 \(u_{k}\) を求める
  5. ノードを新たに加える
Two schemes for exploration

この方法により，空間をrapidly exploreする探索木を構築することができる．

こうなる理由としては，頂点集合のボロノイ領域を考えることで説明がつく．ランダムサンプリングすることで，そのときに 一番大きいボロノイ領域 にサンプリング点がfall intoする確率が大きくなり，そのサンプリング点への最近傍ノードからエッジを伸ばすことでまだ探索されていない領域を探索することになる．インクリメンタルにボロノイ領域を狭めていくことで，グラフは一様に広がる． Kuffer and Lavalle(2000) において，holonomic planning においてはRRTの分布はサンプリングに用いられた確率分布へと収束することが示されている．

RRTのアルゴリズムは以下の通りである．

  1. RANDOM_STATE(): 状態をランダムに選択する
  2. EXTEND(): サンプルされた状態への最近傍ノードをRRTから見つける．このときの"nearest"は状態空間の計量 \(\rho\) により計算される．
  3. NEW_STATE(): 一定時間 \(\Delta t\) だけ制御入力 \(u \in U\) によりサンプルへと移動する．制御入力はランダムに選ばれるか，新しいノードがサンプルに最も近くなるようなものを求める．このようにして得られた新しいノードがcollision-freeであるならば成功．
  4. もしNEW_STATE()が成功したならば， \(x_{new}\) と \(u_{new}\) を得る．これを \(x_{new}\) が \(|x_{new} - x_{goal}| < \epsilon\) を満たすまで続ける．

Rapidly exploring the state space

先ほどの説明から \(\mathcal{X}\) におけるkinodynamic planning に移行するにあたっていくつかの厄介事が起きる．

  1. 次元が高い．
  2. 探索木は \(\mathcal{X}_{free}\) から出てはいけない
  3. ドリフトにより望ましくない動作が実現される可能性がある．
  4. \(\mathcal{X}\) においては最近傍探索のための自然な計量が備わっていない

1つ目の問題に関しては性能を改善するために最近傍探索を近似的に行えばよい(Arya el al. 1998: Indyk and Motwani 1998)．2つ目の問題があると狭い通路の部分でうろうろすることになる．3つ目の問題は，新たなノードの速度項がサンプルされたものとできるだけ等しくなるよう制御入力を選ぶことでいくらかは解決できるかもしれない．4つ目の問題は，性能を最適化したいのであれば，特定のkinodynamic planningの文脈に沿った計量を選択することになるかもしれない．理論的にはこれらの厄介事を全て解決できる完璧な計量は存在している(2つの状態間の最適コスト)．しかしこの計量を求めるのは元々のplanning problemを解くのと同等に難しい．ここでは最低限のヒューリスティックを用いて解決する．そのためより広範なクラスに少し改良をするだけで適用できる．

A Bidirectional Planning Algorithm

RRTの構築の方法は前章で説明したが，path planningを解く際には双方向探索を行えば良い．これは \(x_{init}\) と \(x_{goal}\) から探索木を構築し，共通の状態のノードを求める．双方向探索を用いることの1つの欠点は2つの探索木が接続されるところで軌道が不連続になるということである．軌道を連続にする方法はいくつか考えられる．古典的なシューティング法を用いて，2つ目の軌道の始点に摂動を加えることで1つ目の探索木の終点において接続することが可能かもしれない．

もしこれらの方法で不連続性を取り除くことが不可能ならば，探索木を1つにする代わりに確率 \(p\) で終端状態をサンプリングするようにすれば解が得られる可能性がある．

Experiments with Hovercrafts and Spacecrafts

Dynamic Model, Applying Controls

3次元における剛体の運動方程式は次のようにして表すことができる．

\begin{align*} p &= [p_{x}, p_{y}, p_{z}] \\ q &= [q_{\theta}, q_{x}, q_{y}, q_{z}] \\ v &= [v_{x}, v_{y}, v_{z}] \\ \omega &= [\omega_{x}, \omega_{y}, \omega_{z}] \end{align*}

として

\begin{align*} x(t) = \begin{pmatrix} p(t) \\ q(t) \\ v(t) \\ \omega(t) \end{pmatrix} \end{align*}

ここで要素は全てで13あるが，クオータニオンに関する制約(ノルムが1)により12自由度である．制御入力は力とトルクのペア \((F, \tau)\) であり，状態方程式は以下のようになる．

\begin{align*} \dot{x}(t) &= f(x(t), u(t)) \\ &= \begin{pmatrix} v(t) \\ \hat{\omega}(t) \cdot q(t) / 2 \\ F/M \\ R(t)I^{-1}R(t)^{T}\tau \end{pmatrix} \end{align*}

ここで \(\hat{\omega}(t) = [0, \omega(t)]\) ， \(R(t)\) は回転行列である.

Distance Metric

2つの状態間の計量はそれぞれの重み付け和として定義した．

\begin{align*} \rho(x_{1}, x_{2}) &= w_{p}|p_{1} - p_{2}|^{2} + w_{q}|1 - |q_{1} \cdot q_{2}||^{2} \\ &+ w_{v}|v_{1} - v_{2}|^{2} + w_{\omega}|\omega_{1} - \omega_{2}|^{2} \end{align*}

なおすでに述べたように，最適な計量は2状態間のcost-to-goの差である．

Analysis

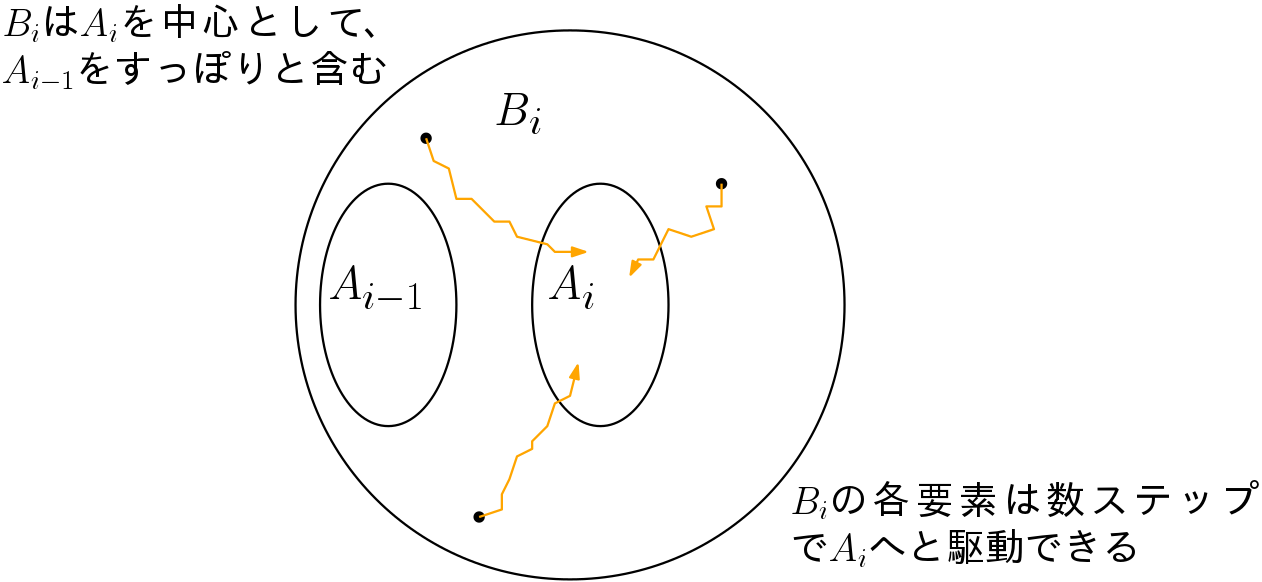
定理1と2でプランナーの収束率，定理3でプランナーの probabilistic complenetess が示される．だがその収束率のパラメータは直接計算しにくいものである． \([A_{0}, A_{1}, \cdots , A_{k}]\) を \(\mathcal{X}\) における attraction sequence と呼ばれる集合列とする． \(A_{0} = x_{init}\) である．以降の各 \(A_{i}\) について basin と呼ばれる集合 \(B{i} \in \mathcal{X}\) が存在し，以下を満たす．

  1. 任意の \(x \in A_{i-1}, y \in A_{i}, z \in \mathcal{X} - B_{i}\) について，計量 \(\rho\) は \(\rho(x, y) < \rho(x, z)\) を満たす．
  2. 任意の \(x \in B_{i}\) について適当な制御入力の系列 \([u_{1}, u_{2}, \cdots , u_{m}]\) が存在して，EXNTED()により \(x\) を \(A_{i} \in B_{i}\) に持っていくことができる．
Attractor Basin

\(\mathcal{A}_{i}\) を中心として \(\mathcal{B}_{i}\) は \(\mathcal{A}_{i-1}\) をすっぽりと含むような円．さらに \(\mathcal{B}_{i}\) は数ステップの制御入力 \(u_{1}, \cdots u_{m}\) で \(\mathcal{A}_{i}\) へと移るような要素の集合である．そして \(k\) 回目のiterationで \(\mathcal{A}_{k} = \mathcal{X}_{\mathrm{goal}}\) となる．

各々のBasin \(B_{i}\) は

  1. \(B_{i}\) の要素は最近傍探索により選ばれることを保証する
  2. その状態が \(A_{i}\) へと駆動される可能性

Attraction Sequence はなるべく大きい方が，そしてiterationの回数 \(k\) はなるべく小さいほうが良い．もし途中に狭い経路を含むと attraction sequence はより長く， \(\mathcal{A}_{i}\) はより狭くなる．この場合経路計画の性能はかなり落ちてしまう．

またkinodynamic planningにおいては計量 \(\rho\) も attraction sequence と planning の性能に大きく影響を与える．

ここで \(p\) を

\begin{align*} p = \min_{i} \mu(A_{i}) / \mu(\mathcal{X}_{\mathrm{free}}) \end{align*}

と定義する．つまりrandomが特定の \(A_{i}\) に入る確率の下限である．

  • 定理

長さ \(k\) のconnection sequence が存在するならば，探索にかかる回数の期待値は \(k / \rho\) である．

  • 証明

もし \(\mathcal{A}_{i-1}\) にRRTの頂点が，\(\mathcal{A}_{i}\) にランダム点 \(x\) が入ったら，次のRRTは \(x\) へと伸びる．なぜならば \(\mathcal{A}_{i}\) に存在している \(x\) を中心とした円の中で，xへの最近傍ノードを含むのは \(\mathcal{A}_{i}\) しかないから． \(A_{i}\) の外のノードは \(\mathcal{B}_{i}\) の定義から絶対に \(\mathcal{A}_{i-1}\) より遠くなる．

よってランダムサンプリングが \(\mathcal{A}_{i}\) に存在する確率は少なくとも \(p\) はある．すなわち， \(\mathcal{A}_{i-1}\) が頂点を含むのなら， \(\mathcal{A}_{i}\) も確率 \(p\) 以上で頂点を含む．最悪の場合，毎回の経路計画は確率 \(p\) で成功するベルヌーイ試行となる．初期状態から目的状態へと至る軌道を求めるためには，試行が \(k\) 回以上成功しないといけない． \(n\) 回の試行で \(k\) 回成功している確率は二項分布に従うから，

\begin{align*} \binom{n}{k} p^{k}(1 - p)^{n-k} \end{align*}

であるから，経路を求めることのできる確率の上界として期待値の \(p / n\) が得られる．

次の定理はiterationを増やすにつれ経路を求めるのに失敗する確率が指数的に減少することを示している．

  • 定理

長さ \(k\) の attraction sequence が存在するなら，ある定数 \(\delta\) が存在して \(n\) 回の iterationの後に解を見つけるのを失敗する確率は高々 \(\exp(-(np - 2k) / 2)\) である．

  • 証明

先ほどの確率過程は，最善で 毎回の成功確率が \(p\) であるベルヌーイ試行で \(k\) 回の成功が起こって経路探索に成功するというものである．

二項分布の裾野の確率を Chernoff上界を用いて評価することができる．Motwani & Raghavan(1995) より \(C\) が二項分布に従うなら， \(\mu = \mathrm{E}[C]\) ， \(\delta \in (0, 1]\) として \(\mathrm{P}[C \le (1 - \delta)\mu] < \exp(\mu \delta^{2} / 2)\) と評価される．ここで \(\delta = 1 - k/np\) である．指数部は

\begin{align*} -\dfrac{1}{2}np + k - \dfrac{k^{2}}{2np} \end{align*}

\(\exp(-k^{2} / np) < 1\) より

\begin{align*} \exp(\mu \delta^{2} / 2) \le \exp(-\dfrac{1}{2}(np - 2k)) \end{align*}

よって探索に失敗する確率は高々:math:exp(-(np - 2k) / 2) である．

  • 定理

これが最後の定理．Probabilistic Completeness が示される．

\(x_{\mathrm{init}}\) と \(x_{\mathrm{goal}}\) がn次元の状態空間において有界な非凸の開領域に存在しているとする．また \(x_{\mathrm{init}}\) を \(x_{\mathrm{goal}}\) まで駆動する入力列 \(u_{1}, u_{2}, \cdots, u_{m}\) が存在すると仮定する(つまり解が存在すると仮定)する．

  • 証明

特定の回数の後のRRTが \(x_{i}\) を頂点として持っているとする． \(\mathrm{Vor}(x_{i})\) を \(x_{i}\) に対するボロノイ領域とする．このとき \(\mu(\mathrm{Vor}(x_{i})) > c_{1}\) となるような \(c_{i}\) が存在する．もしランダムサンプリングが \(\mathrm{Vor}(x_{i})\) に入ったら \(x_{i}\) から伸長が行われるから， \(x_{i}\) は確率 \(\mu(\mathrm{Vor}(x_{i})) / \mu(\mathcal{x}_{\mathrm{free}})\) でサンプリングされる． また \(c_{1}\) に依存する \(c_{2}\) があって適切な \(u_{i}\) が選ばれる確率の下限 \(c_{2}\) を与える． \(x_{i}\) ，\(u_{i}\) が共に選ばれる確率が少なくとも \(c_{2}\) であれば，解軌道の次の段階が求められる確率が1になる傾向がある(めちゃくちゃ直訳っぽい)．

まだ最後の証明が良く分からない．

Designing Metrics

RRTに基づいた手法の主な欠点は性能が計量の選択に大きく依存することである．5章での結果は重み付けユークリッド距離として定義された．しかし計量が変わると特定の問題に対しては性能が大きく変化する．この問題はrandomized人口ポテンシャルフィールドにおけるポテンシャル関数の選択にも似ている．しかしRRTは様々なランダムサンプルへと近づこうとするので，(人口ポテンシャル法の)局所的極小解ほど性能は悪化しない．ポテンシャル関数法では全然だめな計量でも，RRTでは性能をまだ出せるかもしれない．

一般的には理想的な計量を選ぶことができる(実際は計量としての性質を完全には満たしていないので擬計量である)．コスト関数 \(L\) を以下のように定義する．

\begin{align*} L = \int_{0}^{T} l[x(t), u(t)]dt + l_{f}[x(T)] \end{align*}

すると \(x\) と \(x^{\prime}\) の間の最適なcost-to-go(値関数，実際はDPを解いて始めて分かる)は

\begin{align*} \rho^{*}(x, x^{\prime}) = \underset{u(t)}{min} \left( \int_{0}^{T}l[x(t), u(t)]dt + l_{f}[x(T)] \right) \end{align*}

もちろんこれを求めるのは最適制御を解くのと同等に難しいが， \(\rho{*}\) を近似を用いることで性能を上げることができる．