この章では離散時間の有限ホライズンの最適制御を扱っている.状態方程式に対するラグランジュ乗数として随伴変数を導入し,最適制御のハミルトニアンを導入し,変分からオイラーラグランジュ方程式(正準方程式)を導く.最適制御の評価関数値は初期値と終端値の関数であるので,そこから残余コスト(cost-to-go)を導入し,ハミルトンヤコビベルマン方程式(HJB方程式)を導入する.そしてハミルトンヤコビベルマン方程式と最小原理からオイラーラグランジュ方程式が導かれることを示す.離散時間LQを具体例としているので分かりやすい.
システムのダイナミクスが
\begin{align*}
x_{k+1} = f(x_k, u_k, k)
\end{align*}
と表されるとする.初期状態 \(x_0\) が与えられた時,以下の評価関数を最小化する制御系列を求める.
\begin{align*}
J = \phi(x_N) + \sum_{k=0}^{N-1} L(x_k, u_k, k)
\end{align*}
初期状態x0から始めると目的変数は \(x_0, u_0, \cdots u_{N-1}\) であるが,状態方程式を等式制約とみなす.つまり \(x_1, ... x_N\) も目的変数であるとみなし,それらが以下のような関係を満たすと考えるのである.
\begin{align*}
f(x_k, u_k, k) - x_{k+1} = 0
\end{align*}
そこで等式制約付き問題として,評価関数は以下のように表される.
\begin{align*}
\bar{J} = \phi(x_N) + \sum_{k=0}^{N-1}L(x_k, u_k, k) + \lambda_{k+1}^{\text{T}}f(x_k, u_k, k) - \lambda_{k+1}^{\text{T}}x_{k+1}
\end{align*}
ラグランジュ乗数 \(\lambda_k\) のことを特に随伴変数と呼ぶ.式を見やすくするために以下のような関数を導入し,ハミルトン関数と呼ぶ.
\begin{align*}
H(x, u, \lambda, k) = L(x, u, k) + \lambda^{\text{T}}f(x, u, k)
\end{align*}
するとラグランジアンは次のように表される.
\begin{align*}
\bar{J} = \phi(x_N) - \lambda_N^{\text{T}} + H(x_0, u_0, \lambda_1, 0) + \sum_{k=1}^{N-1}H(x_k, u_k, \lambda_{k+1}, k) - \lambda_{k}^{\text{T}}x_k
\end{align*}
この両辺の目的変数に関する全微分(変分)をとることで
\begin{align*}
d\bar{J} = \left( \dfrac{\partial \phi}{\partial x}(x_N) - \lambda_{N}^{\text{T}} \right)dx_N + \sum_{k=1}^{N-1}\left( \dfrac{\partial H_k}{\partial x} - \lambda_{k}^{\text{T}} \right)dx_k + \dfrac{\partial H_k}{\partial x}du_k
\end{align*}
各変分に関する係数がゼロであることが必要条件であるので,それにより以下のオイラーラグランジュ方程式を得る.
\begin{align*}
& x_{k+1} = \left( \dfrac{\partial H}{\partial \lambda} \right)(x_k, u_k, \lambda_{k+1}, k) = f(x_k, u_k, k) \\
& \lambda_k = \left( \dfrac{\partial H}{\partial x} \right)(x_k, u_k, \lambda_{k+1}, k) \\
& \dfrac{\partial H}{\partial u}(x_k, u_k, \lambda_{k+1}, k) = 0 \\
& \lambda_N = \left(\dfrac{\partial \phi}{\partial x} \right)(x_N)
\end{align*}
上の2つの式は解析力学におけるハミルトンの正準方程式に似ているためで,正準方程式と呼ばれる(離散時間であるため第2式にマイナスがついていないが,連続時間で導出すると全く同じ形になる).3つ目の式は最小原理を表しており,この式から陰関数定理により \(u_k\) は \(x_k, \lambda_{k+1}\) の関数として表される.つまり,閉ループにおける状態フィードバックを与える.
解析的に解ける分かりやすい例としてLQ制御が例題として与えられている.評価関数は二次形式であり以下のように表される.
\begin{align*}
J = \dfrac{1}{2}x_{N}^{\text{T}}S_{f}x_N + \sum_{k=0}^{N-1}\dfrac{1}{2}(x_{k}^{\text{T}}Q_{k}x_k + u_{k}^{\text{T}}R_{k}u_k)
\end{align*}
するとハミルトン関数は
\begin{align*}
H(x_k, u_k, \lambda_{k+1}) = \dfrac{1}{2}(x_{k}^{\text{T}}Q_{k}x_{k} + u_{k}^{\text{T}}R_{k}u_{k}) + \lambda_{k+1}^{\text{T}}(A_k x_k + B_k u_k)
\end{align*}
よってオイラーラグランジュ方程式は
\begin{align*}
& x_{k+1} = A_{k}x_{k} + B_{k}u_{k} \\
& \lambda_{k} = Q_{k}x_{k} + A_{k}^{\text{T}}\lambda_{k+1} \\
& u_{k}^{\text{T}}R_{k} + \lambda_{k+1}^{\text{T}}B_{k} = 0 \\
& \lambda_{N} = S_{f}x_{N}
\end{align*}
となる.ここで最適解が \(\lambda_k = S_k x_k\) という形をとると仮定する.ここで \(S_k\) は正定値行列である.これは境界条件を満たしている.詳しい計算は省くが,これは以下のようなRiccati方程式を満たす.
\begin{align*}
S_{k} = (Q_{k} + A_{k}^{\text{T}}S_{k+1}A_{k}) - A_{k}^{\text{T}}S_{k+1}B_{k}(R_{k} + B_{k}^{\text{T}}B_{k})^{-1}B_{k}^{\text{T}}S_{k+1}A_{k}
\end{align*}
この方程式をNから後ろ向きに0まで解くと,
\begin{align*}
u_k = -(R_k + B_{k}^{\text{T}}S_{k+1}B_k)^{-1}B_{k}^{\text{T}}S_{k+1}A_k x_k
\end{align*}
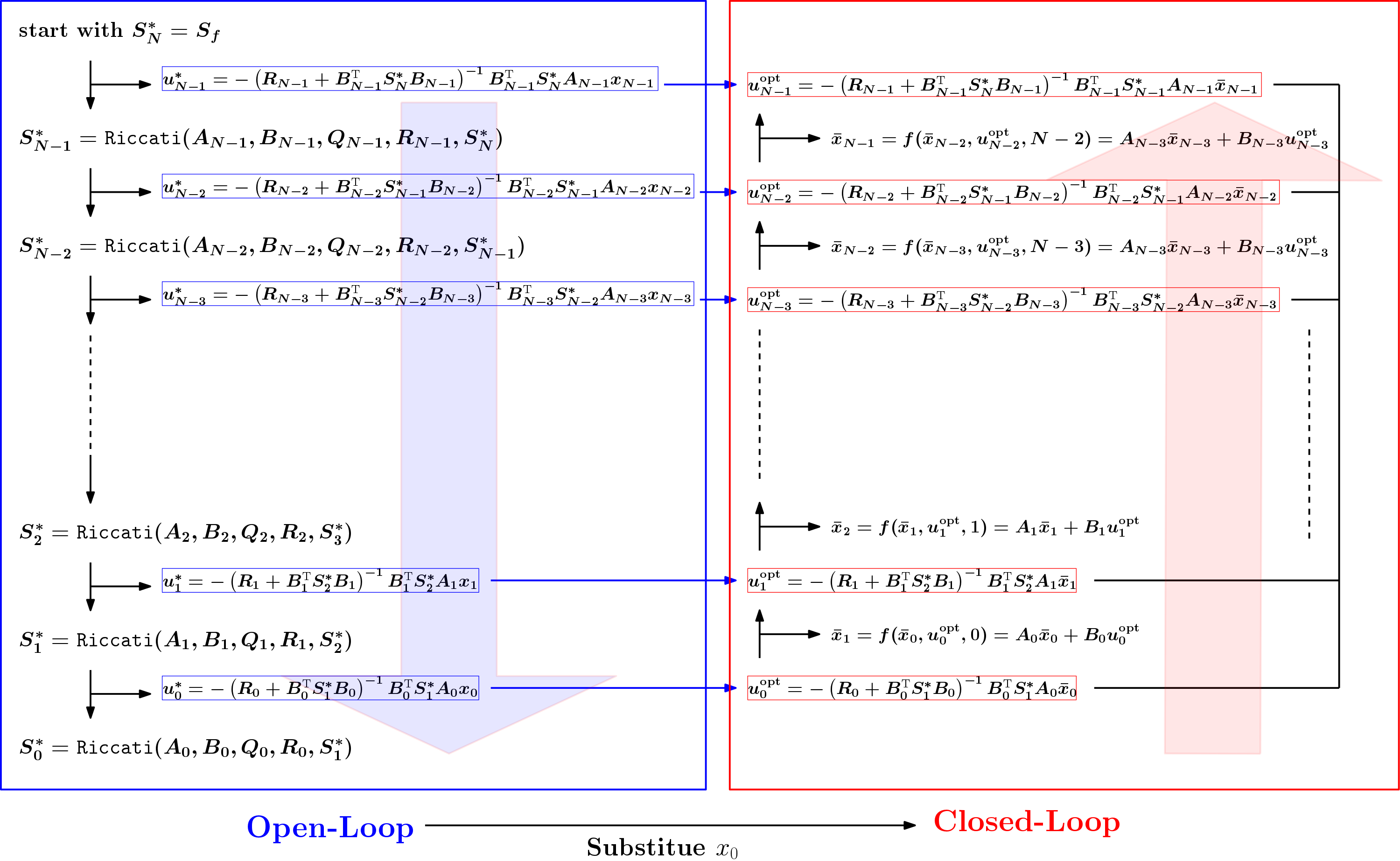
なる閉ループの最適制御入力を求められる.よって実際の初期値 \(x_0\) を用いてこの制御則を用いていけば評価関数を最小化できる.アルゴリズムの様子を以下の図にまとめる.
上の図を見て分かるように,最適制御系列は相互に絡みあった複雑な関係になっているが,基本的に行列パラメータを除いて初期状態 \(x_0\) のみの関数となっている.そのため閉ループの状態フィードバックを用いて \(u_{i}^{\mathrm{opt}}\) を入力していけば評価関数Jは最小値(停留値)になる.したがって評価関数の最小値は もし存在するのならば 初期状態x0の関数として与えられるはずである.つまり「静的な観点」からみるとそれぞれの状態に対してそこから目的状態が与えられると最適な軌道が存在しているということである.そこでこの関数をcost-to-goと呼ぼう.時刻kにおいて状態 \(x_k\) から出発した時の評価関関数を最小にする制御系列が存在するので,cost-to-goは
\begin{align*}
V(x_k, k) = \min_{u_k, ..., u_{N-1}} \left( \phi(x_N) + \sum_{l=k}^{N-1} L(x_l, u_l, l) \right)
\end{align*}
と表される.ただし \(x_{k+1}, \cdots x_{N}\) は自由ではなく,状態方程式に従うので \(x_k\) の関数である.
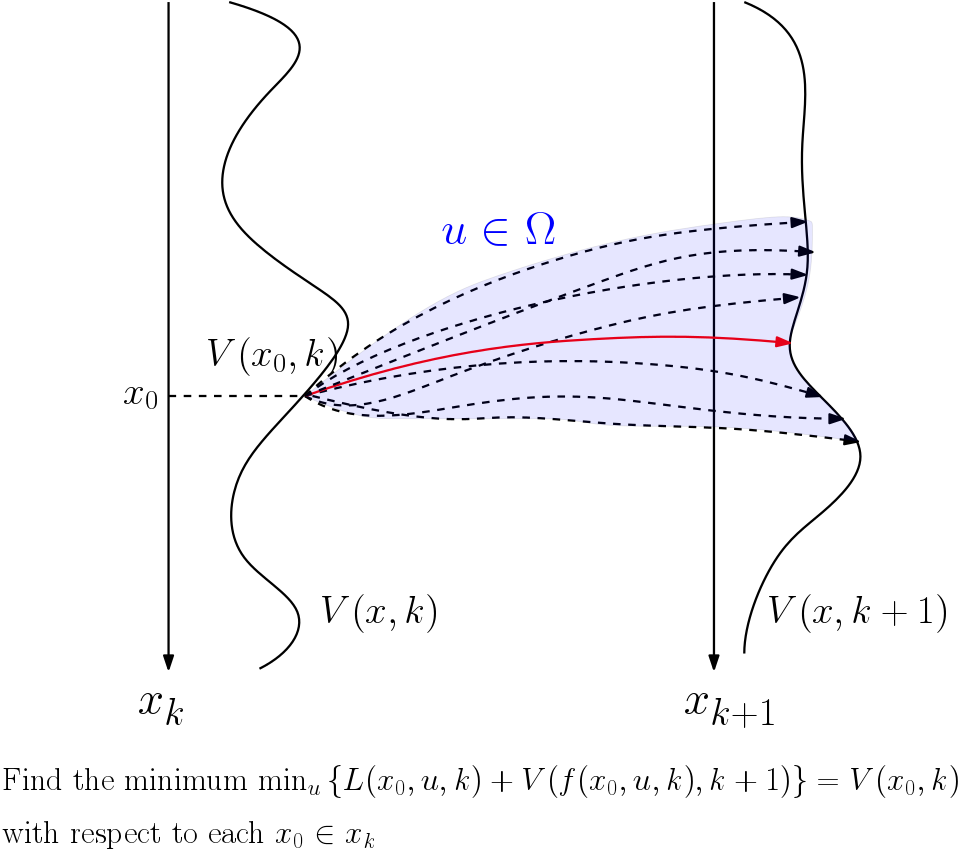
基本的にcost-to-goは「目的地までの最短距離,コスト」なので目標地点から離れれば離れるほど大きな値になる.価値関数は以下のようなBellman方程式に従う.
\begin{align*}
& V(x_k, k) = \min_{u_k}(L(x_k, u_k, k) + V(f(x_k, u_k, k), k+1)) \\
& V(x_N, N) = \phi(x_N)
\end{align*}
\(\phi(x_N)\) は本来 \(u_0, \cdots, u_{N-1}\) まで全ての変数になっている.
価値関数 \(V(x_k, k)\) は「最適制御を \(k = k\) から始めた場合の \(k = N\) までの評価関数の最小値」という意味である.つまり,\(x_k\) が \(u_0, \cdots, u_{k-1}\) の関数であるということを一旦忘れて自由変数とみなし,\(V(x_k, k)\) という \(x_k\) だけの関数とみなすのである.下にイメージ図を示す.
3.3.1 例 離散時間LQ最適制御
線形時不変の系に対してベルマン方程式と終端コストは
\begin{align*}
V(x,k ) &= \min_{u}\left\{ \dfrac{1}{2}(x^{\text{T}}Qx + u^{\text{T}}Ru) + V(Ax + Bu, k+1) \right\} \\
V(x, N) &= \dfrac{1}{2}x^{\text{T}}S_{f}x
\end{align*}
で与えられる.
まず \(k = N\) の場合について計算し, \(V(x, N-1)\) を求めてみる.
\begin{align*}
2V(x, N-1) = \min_{u}\left( x^{\text{T}}Qx + u^{\text{T}}Ru + (Ax + Bu)^{\text{T}}S_{f}(Ax + Bu) \right)
\end{align*}
左辺の括弧の中をuについてまとめると
\begin{align*}
u^{\text{T}}(R + B^{\text{T}}S_{f}B)u + 2x^{\text{T}}A^{\text{T}}S_{f}Bu + x^{\text{T}}(Q + A^{\text{T}}S_{f}A)x
\end{align*}
これをuについて平方完成して最小値を求めると,
\begin{align*}
u_{\mathrm{opt}} = -(R + B^{\text{T}}S_{f}B)^{-1}B^{\text{T}}S_{f}Ax
\end{align*}
において
\begin{align*}
V(x, N-1) = \dfrac{1}{2}x^{\text{T}}(Q + A^{\text{T}}S_{f}A)x - \dfrac{1}{2}x^{\text{T}}A^{\text{T}}S_{f}B(R + B^{\text{T}}S_{f}B)^{-1}B^{\text{T}}S_{f}Ax
\end{align*}
が得られる.両辺を見比べるとRiccati方程式が得られていることが分かる.
3.3.2 ベルマン方程式からのオイラーラグランジュ方程式の導出
ベルマンの最適性の原理は最適性の十分条件を与えるから,最適性の必要条件を与えるオイラーラグランジュ方程式を導出できるはずである.実際にベルマン方程式から得られる最適制御 \(\bar{u}(k) = \bar{u}_{\mathrm{opt}}(\bar{x}(k), k)\) と最適軌道 \(\bar{x}(k)\) がオイラーラグランジュ方程式を満たすことを導出する.
まず全ての \(k= 0, 1, \cdots, N-1\) に対して最適制御と最適軌道はベルマン方程式の右辺の最小値を与えるから
\begin{align*}
-V(\bar{x}(k), k) + L(\bar{x}(k), \bar{u}(k), k) + V(f(\bar{x}(k), \bar{u}(k), k), k+1) = 0
\end{align*}
一方他の状態に対しては \(\bar{u}(k)\) は最適制御ではないから,
\begin{align*}
-V(x(k), k) + L(x(k), \bar{u}(k), k) + V(f(x(k), \bar{u}(k), k), k+1) \geq 0
\end{align*}
よって最適軌道 \(\bar{x}(k)\) は左辺を停留させていることになる.そのため左辺をxに関して偏微分して \(\bar{x}(k)\) を代入すると0になるはずである.
\begin{align*}
& -\dfrac{\partial V}{\partial x}(\bar{x}(k), k) + \dfrac{\partial L}{\partial x}(\bar{x}(k), \bar{u}(k), k) \\
&+ \dfrac{\partial V}{\partial x}(f(\bar{x}(k), \bar{u}(k), k), k+1)\dfrac{\partial f}{\partial x}(\bar{x}(k), \bar{u}(k), k) = 0
\end{align*}
\(\bar{x}(k+1) = f(\bar{x}(k), \bar{u}(k), k)\) を用いると,また終端コストの両辺を偏微分すると
\begin{align*}
& \dfrac{\partial V}{\partial x}(\bar{x}(k), k) = \dfrac{\partial L}{\partial x}(\bar{x}(k), \bar{u}(k), k) + \dfrac{\partial V}{\partial x}(\bar{x}(k+1), k+1)\dfrac{\partial f}{\partial x}(\bar{x}(k), \bar{u}(k), k) = 0 \\
& \dfrac{\partial V}{\partial x}(\bar{x}(N), N) = \dfrac{\partial \phi}{\partial x}(\bar{x}(N))
\end{align*}
ここで
\begin{align*}
\lambda(k) = \left(\dfrac{\partial V}{\partial x} \right)(\bar{x}(k), k)
\end{align*}
という変数 \(\lambda(k)\) を定義すると,なんと先程導出したオイラーラグランジュ方程式が得られている.つまり,随伴変数は,最適軌道上でのcost-to-goの状態変数に関する勾配という幾何学的な意味がある .またベルマン方程式においてuに関する最小値を取る際に,その最小値においては右辺の括弧の中の関数が停留している.そのためそのuに関する編導関数は0になっているはずだから,
\begin{align*}
\dfrac{\partial L}{\partial u}(\bar{x}(k), \bar{u}(k), k) + \dfrac{\partial V}{\partial x}(f(\bar{x}(k), \bar{u}(k), k), k+1)\dfrac{\partial f}{\partial x}(\bar{x}(k), \bar{u}(k), k) = 0
\end{align*}
すなわち,
\begin{align*}
\dfrac{\partial H}{\partial x}\left(\bar{x}(k), \bar{u}(k), \left(\dfrac{\partial V}{\partial x}(\bar{x}(k+1), k+1) , k \right) \right) = 0
\end{align*}
となり,残りの方程式も得られた.