第4章 変分法

この章では変分法について数学的に導入を行っている．

4.1 汎関数の停留条件

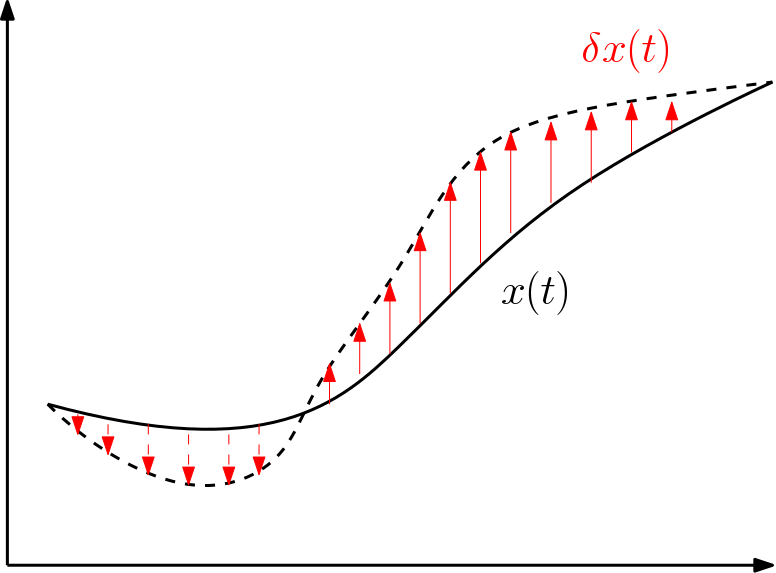
一般に「軌道」と呼ばれるような時間tや弧長変数sでparameterizeされたもの(=関数)を定量化して実数の評価値を返すものを汎関数と呼ぶ．つまり，曲線や曲面，図形のようなドメインからドメインへと返すものを評価して面積や体積を返すもの．従来の微分法では変数はスカラーやベクトル変数のように有限次元であったが，汎関数の引数となる関数は非可算の無限次元の配列である．そのため微分と同じようなことを考える際には関数を微小変化させた「変関数」を考える．一般にx(ｔ)の変関数のことを \(\delta x(t)\) とかく．この \(\delta x(t)\) も関数と同じように時刻や弧長の関数となっている．自分は今までxに \(\delta\) が「左から作用する」と思っていたのだが，そうではなく \(\delta x\) で「1つの関数」である．

/_images/variation_function

一般に汎関数は以下のように積分で表される．

\begin{align*} J[x(t)] = \int_{t_0}^{t_f}L(x(t), \dot{x}(t), t) dt \end{align*}

変分に関してもテイラー展開を考えることができる． ある許容曲線 \(x^{*}(t)\) が汎関数 \(J[(t)]\) を停留させているとする．そこから変関数 \(\delta x(t)\) だけ変化したとすると

\begin{align*} & L(x^{*}(t) + \delta x(t), \dot{x}^{*}(t) + \delta \dot{x}(t), t) \\ & = L + \begin{bmatrix} \dfrac{\partial L}{\partial x} & \dfrac{\partial L}{\partial \dot{x}}\end{bmatrix} \begin{bmatrix} \delta x \\ \delta \dot{x} \end{bmatrix} + \dfrac{1}{2}\begin{bmatrix} \delta x^{\text{T}} & \delta \dot{x}^{\text{T}} \end{bmatrix} \begin{bmatrix} \dfrac{\partial^{2} L}{\partial x^{2}} & \dfrac{\partial^{2} L}{\partial x \partial \dot{x}} \\ \dfrac{\partial^{2} L}{\partial \dot{x} \partial x} & \dfrac{\partial^{2} L}{\partial \dot{x}^{2}} \end{bmatrix} \begin{bmatrix} \delta x \\ \delta \dot{x} \end{bmatrix} \end{align*}

よって汎関数も

\begin{align*} J[x^{*} + \delta x] = J[x^{*}] + \delta J[x^{*}, \delta x] + \delta^{2}J[x^{*}, \delta x] \end{align*}

だけ変化する．それぞれの項を1次の変分，２次の変分と呼ぶ．

有限次元との違い

有限次元の場合は2次系式の部分の行列，ヘッセ行列が正定値であれば孤立局所解であることが言えた．しかし変分問題は無限次元であるため，必ずしも正定値であるだけでは不十分であることがある．より詳しく見てみよう． 許容変分が正の定数 \(\alpha\) を用いて \(\delta x = \alpha y\) のようにして表されるとする．すると

\begin{align*} J[x^{*} + \alpha y] = J[x^{*}] + \alpha \delta J[x^{*}, y] + \alpha^{2} \delta^{2}J[x^{*}, y] \end{align*}

\(x^{*}\) で孤立局所解をとるとすると \(\delta J[x^{*}, y] = 0\) であることが必要である．さらに \(\delta J[x^{*}, y] = 0\) であるならば \(\alpha\) を十分小さくすることで \(J[x^{*} + \alpha y] - J[x^{*}]\) の符号は \(\alpha^{2} \delta^{2} J[x^{*}, y]\) と等しくなるから \(\delta^{2} J[x^{*}, y] \leq 0\) でなければならない．この項はヘッセ行列の2次形式を無限次元に拡張したものとしてみなせるため，固有値も無限個存在している(固有関数)．そのため \(\delta^{2} J[x^{*}, y]\) が正定だとしてもいくらでも0にちかい固有値が存在している可能性がある．そのため2次の十分条件ではある正の定数 \(\gamma\) を用いて \(\delta^{2} J[x^{*}, y] > \gamma\) である必要があり，有限次元における正定値性よりも強い条件が要求される．

オイラーの方程式

\begin{align*} \dfrac{d}{dt}\left( \dfrac{\partial L}{\partial \dot{x}} \right) - \dfrac{\partial L}{\partial x} = 0 \end{align*}

終端値 \(x(t_f)\) が自由であるならば

\begin{align*} \dfrac{\partial L}{\partial \dot{x}}(x(t_f), \dot{x}(t_f), t_f) = 0 \end{align*}

も課される．これをtransversality condition(横断性条件)という．