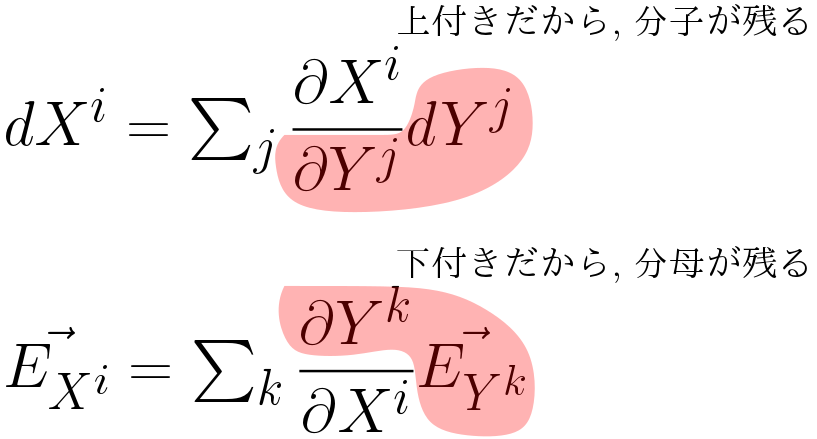付録

先に数学的な基礎から述べておく．個人的に「なるほどな」と思ったのはルジャンドル変換の項である．

ルジャンドル変換

ルジャンドル変換は，関数の引数を \(x\) から \(d/dx\) に変更する際に，関数から得られる「情報」を保存するために，関数 \(f(x)\) を変換する方法．この「情報」とは「その関数の切片に関する情報」である．

もしルジャンドル変換をしなかったら?

aを定数として以下のような関数

\begin{align*} f(x) = (x - a)^{2} \end{align*}

を考えよう．そこでxによる微分

\begin{align*} p_x = \dfrac{\partial f}{\partial x} = 2(x - a) \end{align*}

を独立変数に新たにとろう．そしてfを以下のように書き換える．

\begin{align*} \tilde{f} = \dfrac{p_{x}^{2}}{4} \end{align*}

ここで，関数fは量としては変わっていないものの関数の形(写像としては)が変わっているので，本来は \(\tilde{f}\) と書くべきではある．

しかし，変換後の \(\tilde{f}\) にはaに関する情報が入っていない．そのため， \(f(x) = (x - a)^{2}\) でも \(f(x) = (x - b)^{2}\) でも写像として \(\tilde{f}\) はそれに応じて変化しない(から問題である)．

ルジャンドル変換

もし関数の引数を元々の引数の微分に置き換えてもこのような「情報」を保存するためには以下のように変換すれば良い．

\begin{align*} \tilde{f}(p_x) = f(x) - xp_x \end{align*}

ただし，xを \(p_x\) について解いて代入する． つまり，元々の関数から，(微分に用いる変数) x (fをそれで微分したもの)を引くわけである．

また逆変換は上の式を \(p_x\) で偏微分して

\begin{align*} x = -\dfrac{\partial \tilde{f}}{\partial p_x} \end{align*}

とした式である．

上の例で計算すると．

\begin{align*} \tilde{f}(p_x) = (x - a)^{2} - xp_x = \dfrac{p_{x}^{2}}{4} - \left( \dfrac{p_x}{2} + a \right)p_x = -\dfrac{p_{x}^{2}}{4} - ap_x \end{align*}

一方ここから逆変換すると

\begin{align*} x = -\dfrac{\partial \tilde{f}}{\partial p_x} = \dfrac{p_x}{2} + a \end{align*}

より

\begin{align*} f(x) = -(x - a)^{2} - 2a(x - a) + 2x(x - a) = (x - a)^{2} \end{align*}

より元に戻る．

ルジャンドル変換で独立変数の関係をうまく行える理由を全微分を求めて示しておこう．\(f(x, y)\) としてみなすと

\begin{align*} df = \dfrac{\partial f}{\partial x}dx + \dfrac{\partial f}{\partial y}dy \end{align*}

ただしそれぞれの偏微分ではｙとxが一定になっている．一方 \(\tilde{f} = f - xp_x\) については

\begin{align*} d\tilde{f} = \dfrac{\partial f}{\partial x}dx + \dfrac{\partial f}{\partial y}dy - (p_x dx + x dp_x) = \dfrac{\partial f}{\partial y}dy - x dp_x \end{align*}

となる．よって関数の変換の前後においてxを一定としたときのfのy微分と， \(p_x\) を一定として \(\tilde{f}\) をy微分した時の値が等しくなる．

\begin{align*} \left. \dfrac{\partial f}{\partial y}\right|_x = \left. \dfrac{\partial \tilde{f}}{\partial y} \right|_{p_x} \end{align*}

ある意味，変換の前後で \(x\) と \(p_x\) の立場が対等になっていると言える．

解析力学ではラグランジアン \(L\) を \(\dot{q}\) で偏微分した値として定義される一般化運動量

\begin{align*} p = \dfrac{\partial L}{\partial \dot{q}} \end{align*}

をラグランジアンの引数 \(\dot{q}\) と変換するために，次のようにルジャンドル変換を行う．

\begin{align*} H(q, p, t) = \dot{q}p - L(q, \dot{q}, t) \end{align*}

座標系に関して

まだ曲線座標で表される点がユークリッド空間に存在していることを仮定しているが，微分幾何学っぽくなってきた．曲線座標上の座標値はユークリッド空間での \((x_1, x_2, \cdots x_D)\) には対応していない．ただし，原点は共有しているものとする．

曲線座標とベクトル

曲線座標を用いてD次元ユークリッド座標における点が \((X^1, X^2, \cdots, X^D)\) 表されているとする．誤解を招かないよう一応書いておくと，これはx, y, z ,,,座標の値を順番に表示したものではない．実際は

\begin{align*} x &= r \cos \theta \\ y &= r \sin \theta \end{align*}

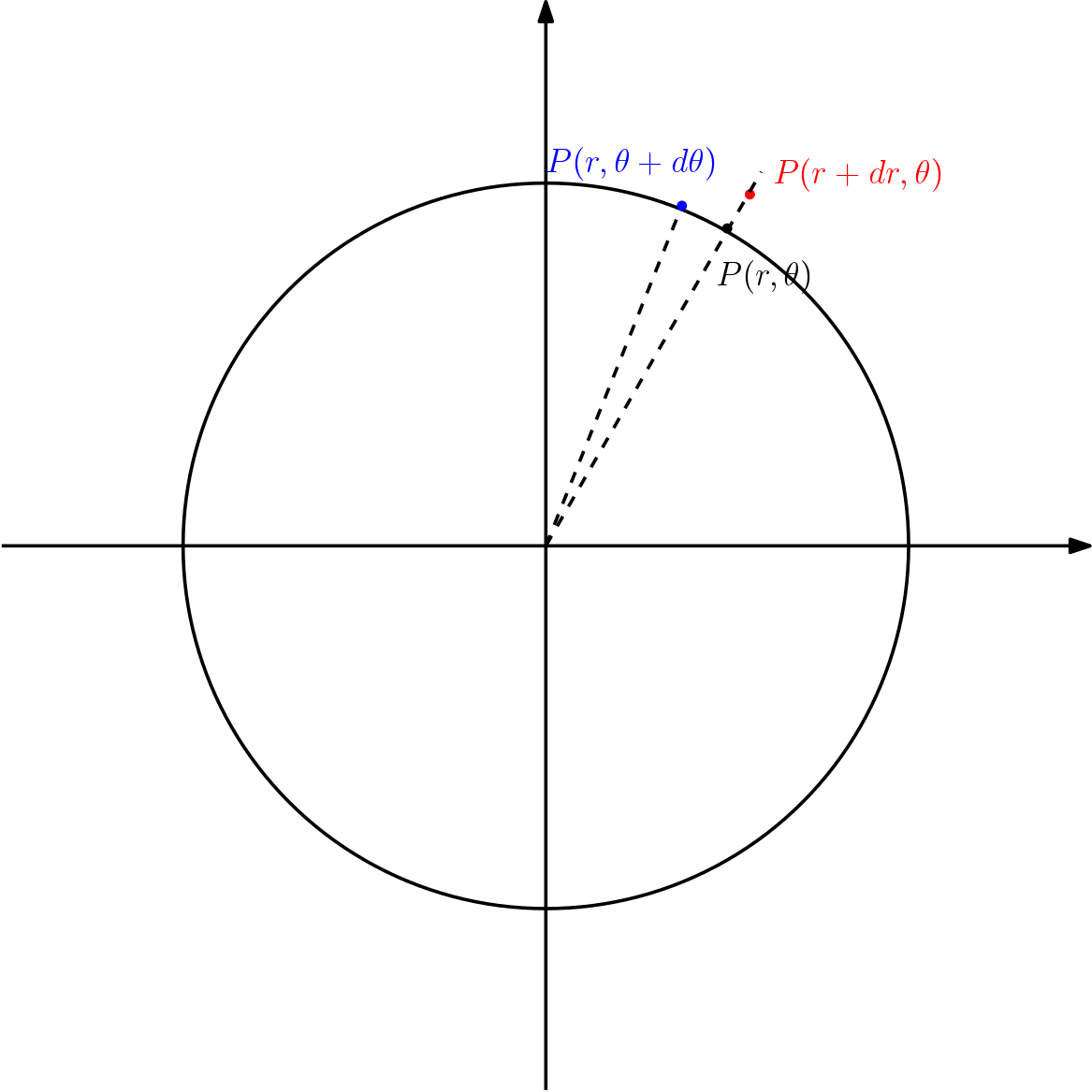
のように曲線座標からユークリッド空間へとマッピングされている．曲線座標における基底ベクトルを次のように定義する．

\((X^1, X^2, \cdots, X^D)\) のうち \(X^i\) だけを \(dX^i\) だけ変化させることによる ユークリッド空間上での移動ベクトル を \(\vec{E}_i\) と定義する．

例えば2次元の極座標では，下の図のようになる．

2dpolar.png

変位ベクトル \(d\vec{x}\) は以下のように書ける．

\begin{align*} d\vec{x} = \begin{cases} dx\vec{e_x} + dy\vec{e_y} \\ dr\vec{e_r} + rd\theta \vec{e_{\theta}} \end{cases} \end{align*}

よって微小変位を取り出したものが

\begin{align*} \vec{E_r} &= \vec{e_r} \\ \vec{E_{\theta}} &= r \vec{e_{\theta}} \end{align*}

となる．微小変位は座標系によらない量であるため，これによりそれを以下のように表現できる．

\begin{align*} d\vec{x} = dx\vec{E_x} + dy\vec{E_y} = dr\vec{E_r} + d\theta\vec{E_{\theta}} \end{align*}

つまり，座標系による違いは各 \(\vec{E}\) に吸収されている．

もし座標変換により

\begin{align*} dX^i = \sum_{j}\dfrac{\partial X^i}{\partial Y^j}dY^j \end{align*}

と変換されたとき，基底の方はその逆行列で

\begin{align*} \vec{E_{X^i}} = \sum_{k}\dfrac{\partial Y^k}{\partial X^i}\vec{E_{Y^k}} \end{align*}

と変換される．上付きと下付きのイメージ図を下に示す．

upper_lower.png

ここで \(\vec{E_{X^i}}\) に双対なベクトルとして \(\vec{E^{X^i}}\) を

\begin{align*} \vec{E_{X^i}} \cdot \vec{E_{X^i}} = \delta_{ij} \end{align*}

を満たすものとして定義する．

すると

\begin{align*} \nabla = \vec{E^{X^i}} \dfrac{\partial}{\partial X^i} \end{align*}

として表される．たとえ以下のように3次元であっても．

\begin{align*} \nabla = \begin{cases} \vec{E^{x}} \dfrac{\partial}{\partial x} + \vec{E^{y}} \dfrac{\partial}{\partial y} + \vec{E^{z}} \dfrac{\partial}{\partial z} \\ \vec{E^{r}} \dfrac{\partial}{\partial r} + \vec{E^{\theta}} \dfrac{\partial}{\partial \theta} + \vec{E^{\phi}} \dfrac{\partial}{\partial \phi}\end{cases} \end{align*}