\begin{align*}
S[x(t)] = \int_{t_0}^{t_f}dt\left( \dfrac{m}{2}|\dot{x}(t)|^{2} - V(x(t)) \right)
\end{align*}
まず始めに到着点を変化させると主関数がどのように変化するかを求める.そしてそこからさらに運動量の保存則を(ラグランジアンにおける循環座標を利用することなく)発見する.
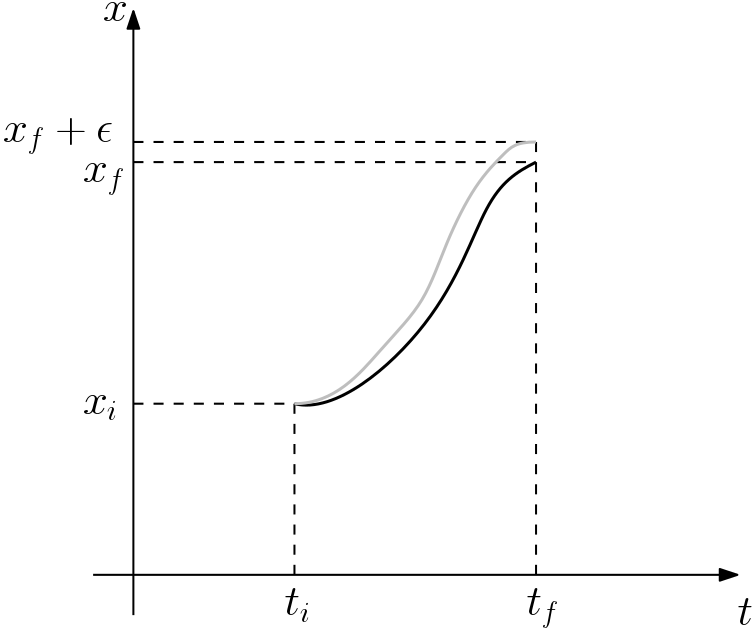
到着点を \(x_{f} \to x_{f} + \epsilon\) とすると,それに応じて経路自体も移動する.変化した経路 \(x(t) + \delta x(t)\) 自体もEL方程式を満たす.それによる作用の変化 \(\delta \bar{S}\) は
\begin{align*}
\int_{t_i}^{t_f}dt L(x_t, \dot{x_t}) \to \int_{t_i}^{t_f}dt L(x_t + \delta x_t, \dot{x_t} + \delta \dot{x_t})
\end{align*}
2つ目の式を展開すると
\begin{align*}
& \int_{t_i}^{t_f}dt L(x_t + \delta x_t, \dot{x_t} + \delta \dot{x_t}) \\ &= \int_{t_i}^{t_f}dt \left( L(x_t, \dot{x_t}) + \delta x_t \cdot \dfrac{\partial L}{\partial x_t} + \delta \dot{x_t} \cdot \dfrac{\partial L}{\partial x_t} \right)
\end{align*}
となるから変化量は
\begin{align*}
\delta \bar{S}(x_f, x_i) = \int_{t_i}^{t_f}dt\left( \delta x_t \cdot \dfrac{\partial L}{\partial x_t} + \delta \dot{x_t} \cdot \dfrac{\partial L}{\partial \dot{x_t}} \right)
\end{align*}
部分積分を行い,またEL方程式を使って項を消すと
\begin{align*}
\delta \bar{S} = \left. \delta x_t \cdot \dfrac{\partial L}{\partial \dot{x_t}} \right|_{t_f} - \left. \delta x_t \cdot \dfrac{\partial L}{\partial \dot{x_t}} \right|_{t_i}
\end{align*}
\(\delta x_t\) は出発点では0,到着点で \(\epsilon\) としていたので
\begin{align*}
\dfrac{\partial \bar{S}}{\partial x_f} = \dfrac{\partial L}{\partial \dot{x_t}} = \left. m\dot{x} \right|_{t_f}
\end{align*}
となる.
運動量保存則の導出
上の計算では変分は出発点では0であったが,出発点でも到着点でも等しい,つまり一様に座標をシフトさせたとする.ここで,作用に \(x \to x + \epsilon\) なる変換に不変性があるとする.すると主関数の値は変化しないので
\begin{align*}
m \left. \dot{x} \right|_{t_f} - m \left. \dot{x} \right|_{t_i} = 0
\end{align*}
となり運動量保存則が導かれる.
空間座標 \(x\) を \(x + \epsilon\) とずらした時の不変性から運動量保存則が出るのであれば,時間座標を \(t\) から \(t + \epsilon\) とずらした時に作用が不変だとしたら,何が導かれるのだろうか?すなわち,
\begin{align*}
\int_{t_i}^{t_f}dt L(x_t, \dot{x_t}) \rightarrow \int_{t_i}^{t_f + \epsilon} dt L(x_t + \delta x_t, \dot{x} + \delta \dot{x_t})
\end{align*}
と到着時間を少しずらしても作用が不変だった場合である.
警告
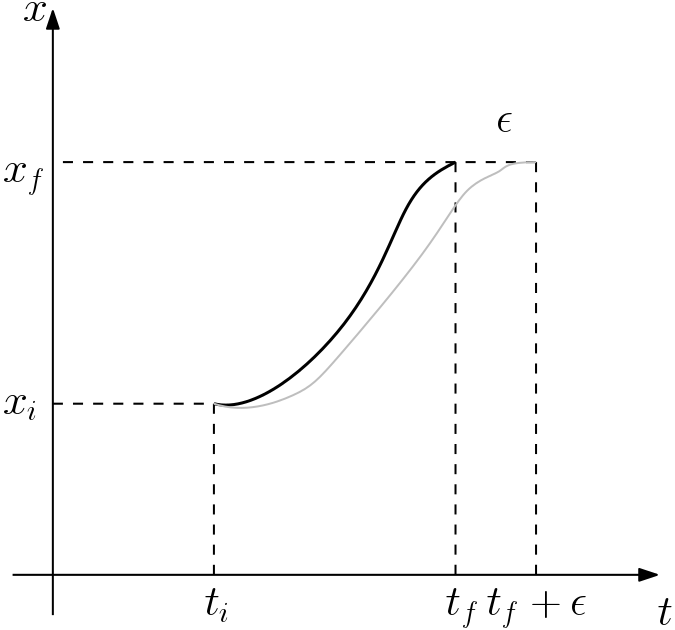
到着点は固定している.そのため少し遅れてやってくる.
この場合も到着時間が変化することにより経路自体も変化する.図のようにEL方程式を満たすon-shellの2つの経路があるとして,その際のハミルトンの主関数の値を
\begin{align*}
\int_{t_f}^{t_f + \epsilon}dt L(x_t + \delta x_t, \dot{x} + \delta \dot{x_t}) + \int_{t_i}^{t_f} dt L(x_t + \delta x_t, \dot{x} + \delta \dot{x_t})
\end{align*}
のようにして2つに分ける.第一項は積分領域が微小であるから, \(\epsilon L(x(t_f), \dot{x}(t_f))\) という値になる.第二項については
\begin{align*}
\delta x \cdot \left. \dfrac{\partial L}{\partial \dot{x}} \right|_{t_f} - \delta x \cdot \left. \dfrac{\partial L}{\partial \dot{x}} \right|_{t_i}
\end{align*}
となる.しかし今回は \(\delta x(t_i) = 0\) ではあるが \(\delta x(t_f) = \epsilon\) ではない.
この場合図から, \((x \delta x)(t_f)\) はあと \(\epsilon\) だけ時間経過したらもともとの到着点である \(x(t_f)\) に到着する予定である地点である.そのため,
\begin{align*}
x(t_f) = x(t_f + \epsilon) + \delta x(t_f + \epsilon)
\end{align*}
が成立する.これをTaylor展開して
\begin{align*}
x(t_f) = x(t_f) + \epsilon \dot{x}(t_f) + \delta x(t_f) + \epsilon \delta \dot{x}(t_f)
\end{align*}
となり,その最終項は2次の微小量である.ここから
\begin{align*}
\delta x(t_f) = \epsilon \dot{x}(t_f)
\end{align*}
が得られる.よってまとめると
\begin{align*}
\delta \bar{S} = \epsilon \left. L \right|_{t_f} - \epsilon \dot{x} \cdot \left. \dfrac{\partial L}{\partial \dot{x}} \right|_{t_f} = -\epsilon \left. \left( \dot{x} \cdot \dfrac{\partial L}{\partial \dot{x}} - L \right)\right|_{t_f}
\end{align*}
ラグランジアンが \(L = \dfrac{m}{2}|\dot{x}|^{2} - V(x)\) であるとするとこの括弧の中の量はハミルトニアン \(H = \dfrac{m}{2}|\dot{x}|^{2} + V(x)\) である.というより,そもそもハミルトニアンの定義になっている.
注釈
「この座標の並進に関して作用が不変であるからこの量が保存する」ということを言うためには,その座標を \(\epsilon\) だけずらした際の作用のズレ \(\delta \bar{S}\) を計算して,そのズレにおける \(\epsilon\) に関する一次の項の係数をゼロとすればよい,すなわち保存量とすればよい.
例題
以下のラグランジアンに対応する保存量をネーターの定理から見つけよ.
\begin{align*}
L = \dfrac{\dot{x}}{\dot{y}} - k\dfrac{x}{y}
\end{align*}
このラグラジアンはxとyの同次式になっている.そのため \(x \rightarrow \epsilon x\) , \(y \rightarrow \epsilon y\) なる変換に対して不変であると考えられる.これに対するラグランジアンの変化を計算してみよう.
\begin{align*}
\delta L &= \dfrac{\dot{x} + \delta \dot{x}}{\dot{y} + \delta \dot{y}} - k\dfrac{x + \delta x}{y + \delta y} - \dfrac{\dot{x}}{\dot{y}} + k\dfrac{x}{y} \\
&= (\dot{x} + \delta \dot{x})\dfrac{1}{\dot{y}}\left( 1 - \dfrac{\delta \dot{y}}{\dot{y}} \right) - k(x + \delta x)\dfrac{1}{y}\left( 1 - \dfrac{\delta y}{y} \right) - \dfrac{\dot{x}}{\dot{y}} + k\dfrac{x}{y} \\
&= \dfrac{\dot{y}\delta \dot{x} - \dot{x}\delta \dot{y}}{\dot{y}^{2}} + \dfrac{x \delta y - y \delta x}{y^2}k \\
\end{align*}
ここで \(\delta x = \epsilon x\) , \(\delta y = \epsilon y\) を代入すると
\begin{align*}
\delta L = 0
\end{align*}
となる.よってネーターの定理において \(J = 0\) である.したがって以下の
\begin{align*}
\dfrac{L}{\partial \dot{x}}\epsilon x + \dfrac{L}{\partial \dot{y}}\epsilon y - J(=0)
\end{align*}
の \(\epsilon\) の一次の項
\begin{align*}
\dfrac{\partial L}{\partial \dot{x}} x + \dfrac{\partial L}{\partial \dot{y}} y = \dfrac{x}{\dot{y}} - \dfrac{\dot{x}y}{\dot{y}^{2}}
\end{align*}
が保存量である.