正準変換は,変換後も正準方程式が成立するようなものである.オイラーラグランジュ方程式は任意の点変換 \(Q(q)\) で方程式は共変的であったが,ハミルトン形式の点変換 \(Q(q, p), P(q, p)\) は一般には共変的ではない.
詳しい計算はここでは省く.結論から書くと2次元の場合
\begin{align*}
\{ Q, P \} = \dfrac{\partial Q}{\partial q}\dfrac{\partial P}{\partial p} - \dfrac{\partial Q}{\partial p}\dfrac{\partial P}{\partial q} = 1
\end{align*}
のように変数変換のヤコビアンが1になるならば正準変換である.多変数の場合は後で述べる.これは位相空間の積分要素が以下のように保存されるということである.
\begin{align*}
dpdq = dPdQ
\end{align*}
ここも2次元の場合について述べる.
- \(q\) を \(\alpha\) 倍したときに \(p\) は \(1 / \alpha\) 倍される.\(Q = \alpha q, P = p / \alpha\)
- \(p\) を \(p + bq\) のように平行四辺形の高さを変えないように変をずらす. \(Q = q, P = p + bq\)
- \(q, p\) を \(\theta\) だけ回転させる.
一つ一つについて計算してみる.
\begin{align*}
\dfrac{\partial Q}{\partial q}\dfrac{\partial P}{\partial p} - \dfrac{\partial Q}{\partial p}\dfrac{\partial P}{\partial q} = \alpha \cdot \dfrac{1}{\alpha} - 0 \cdot 0 = 1
\end{align*}
\begin{align*}
\dfrac{\partial Q}{\partial q}\dfrac{\partial P}{\partial p} - \dfrac{\partial Q}{\partial p}\dfrac{\partial P}{\partial q} = 1 \cdot 1 - 0 \cdot b = 1
\end{align*}
\begin{align*}
\dfrac{\partial Q}{\partial q}\dfrac{\partial P}{\partial p} - \dfrac{\partial Q}{\partial p}\dfrac{\partial P}{\partial q} = \cos \theta \cdot \cos \theta - \sin \theta \cdot (-\sin \theta) = 1
\end{align*}
新しい正準座標でのポアソン括弧は古い正準座標とどのような関係があるのだろうか.
\begin{align*}
\{ A, B \}_{Q, P} = \dfrac{\partial A}{\partial Q}\dfrac{\partial B}{\partial P} - \dfrac{\partial B}{\partial Q}\dfrac{\partial A}{\partial P}
\end{align*}
\begin{align*}
\{ A, B \}_{q, p} = \dfrac{\partial A}{\partial q}\dfrac{\partial B}{\partial p} - \dfrac{\partial B}{\partial q}\dfrac{\partial A}{\partial p}
\end{align*}
実はこれらは
\begin{align*}
\{ A, B \}_{Q, P} \{ Q, P \}_{q, p} = \{ A, B \}_{q, p}
\end{align*}
を満たす.するとこれを用いて新しい正準方程式が形を変えないことを簡単に示せる.
一般の \((q, p)\) の関数 \(A(q, p)\) について
\begin{align*}
\dfrac{d A(q, p)}{dt} = \{ A(q, p), H \}_{(q, p)}
\end{align*}
が成立することは分かっている.そして \(J = 1\) であれば \(\{ A, H \}_{(q, p)} = \{ A, H \}_{(Q, P)}\) が成立するから
\begin{align*}
\dfrac{d A(q(Q, P), p(Q, P))}{dt} = \{ A(q(Q, P), p(Q, P)), H \}_{(Q, P)}
\end{align*}
よって関数として \(Q, P\) を代入すれば
\begin{align*}
\dfrac{dP}{dt} = \{ P, H \}_{Q, P}, \quad \dfrac{dQ}{dt} = \{ Q, H \}_{Q, P}
\end{align*}
が得られる.今考えている1次元問題では,基本ポアソン括弧で意味があるのは \(\{ Q, Q \}\) , \(\{ Q, P \}\) , \(\{ P, P \}\) のうち \(\{ Q, P \}\) だけである.他の2つはポアソン括弧の性質から自明である.
正準変換は位相空間での面積を変えない座標変換であった.一方,リウヴィルの定理が主張しているのも,位相空間のハミルトニアンフローに沿った時間発展も面積要素を保存するということだった.そこで少し思考の飛躍をして,「正準変換も位相空間における微分と似たものであるポアソン括弧を使って表現できないだろうか?」と考える.つまり,
\begin{align*}
p(t + \delta t) &= p(t) + \delta t \cdot \{p, H\} \\
q(t + \delta t) &= q(t) + \delta t \cdot \{q, H\}
\end{align*}
の真似をして, \(\epsilon\) を微小なパラメータとして
\begin{align*}
P = p + \epsilon\{p, G\}, \quad Q = q + \epsilon \{q, G\}
\end{align*}
とすればこれは自動的に面積を変化させない変換になっている(リウヴィルの定理でハミルトニアンだったところをGにするだけ).この関数 \(G\) のことを生成子と呼ぶ.実際この変換のポアソン括弧を計算してみると
\begin{align*}
\{Q, P\} &= \{q + \epsilon\{q, G\}, p + \epsilon\{p, G\} \} \\ &= \{q, p \} + \epsilon \{q, \{p, G\} \} + \epsilon\{\{q, G\}, p\} + O(\epsilon^2)
\end{align*}
となるが,ヤコビ恒等式より
\begin{align*}
\{q, \{p, G\} \} + \{\{q, G\}, p\} = -\{G, \{q, p\}\} = -\{G, 1\} = 0
\end{align*}
が得られるから(定数とのポアソン括弧は0),確かに
\begin{align*}
\{Q, P\} = \{q, p\} - \epsilon\{G, \{q, p\}\} = 1
\end{align*}
が得られて正準変換になっている.
ここでも原点に立ち返って変分原理から正準変換を導出してみよう.ここでは ラグランジアンの不定性が母関数として 活躍する.
\((q, p) \rightarrow (Q, P)\) という正準変換を行った時,作用も
\begin{align*}
\int \left( p \dot{q} - H(q, p) \right) dt \rightarrow \int \left( P\dot{Q} - H(q(Q, P), p(Q, P))\right) d t
\end{align*}
へと変化する.それでも正準方程式が変化しないためにはどんな条件が必要だろうか? 変数は \(p\dot{q}\) から \(P \dot{Q}\) へと変化が起こっていて,しかも \(Q\) は \(Q(q, p)\) として書けるから \(P\dot{Q}\) の中には \(\dot{p}\) が入ってくる(note).
注釈
\(Q\) が \(p\) を含まない場合はラグランジュ形式における点変換である.よってラグランジュ方程式は共変的であり,作用が保存するのは当然であるのだが,今回は \(Q(q, p)\) のようにpの関数になっているから,作用は変化してしまう.
よってラグランジアンの値自体も変化する.よって
\begin{align*}
\int \left( p \dot{q} - H(q, p) \right) dt \rightarrow \int \left( P\dot{Q} - H(q(Q, P), p(Q, P)) + \dfrac{dG}{dt} \right) d t
\end{align*}
のように「表面項」が付け加わる.これは 正準変換に伴いラグランジアンが増えてしまった分を補償している とも言える.この関数 \(G\) を決めることは正準変換を指定することに対応しているので特に正準変換の母関数と呼ばれている.
位相空間で回転を行う正準変換
\begin{align*}
(q, p) \rightarrow (Q, P) = (q\cos \theta + p\sin \theta, -q\sin \theta + p \cos \theta)
\end{align*}
を考えてみよう.
\begin{align*}
P\dot{Q} + \dfrac{dG}{dt} &= p \dot{q} \\
(p \cos \theta - q \sin \theta)(\dot{p}\sin \theta + \dot{q} \cos \theta) + \dfrac{dG}{dt} = p\dot{q} \\
(p\dot{p} - q\dot{q})\cos \theta \sin \theta - p\dot{q}(1 - \cos^{2} \theta) - q \dot{p}\sin^{2} \theta + \dfrac{dG}{dt} &= 0 \\
\dfrac{1}{2}\dfrac{d(p^2 - q^2)}{dt}\cos \theta \sin \theta - \dfrac{d(pq)}{dt} \sin^{2} \theta + \dfrac{dG}{dt} &= 0
\end{align*}
よって
\begin{align*}
G = -\dfrac{1}{2}(p^2 - q^2)\cos \theta \sin \theta + pq \sin^{2}\theta
\end{align*}
が得られる.
注釈
ハミルトニアンの値は変わらないが, \(p\dot{q}\) の項はずれが生じる.等しくなるようにずれを求めているだけ.むしろこの関数 \(G\) がきちんと見つかるのか,そしてこの関数から正準変換に関する情報を引き出せるだけの情報があるのか,という視点の方が重要.
結局母関数は作用の積分を等しくするために
\begin{align*}
p\dot{q} = P\dot{Q} + \dfrac{dG}{dt}
\end{align*}
が成立するようズレを計算してあげたものである.この式から
\begin{align*}
pdq = PdQ + dG
\end{align*}
が得られる.
注釈
数学力が乏しいため,「単純に約分した」というようにしか今は見ることしかできない.
基本的に \(G\) は \(q, p, Q, P\) どの変数で表しても良いのだが, \(Q = Q(q, p)\) , \(P = P(q, p)\) のような関係があるので,自由度は2つだけである.
警告
もしそうでなければ(自由度が2でなければ) \(dG = \dfrac{\partial G}{\partial q}dq + \dfrac{\partial G}{\partial p}dp + \dfrac{\partial G}{\partial Q}dQ + \dfrac{\partial G}{\partial P}dP\) のようになってしまい, \(dq, dp, dQ, dP\) が独立でなくなるため各係数を比較することができない.
なので2つを選んで残り2つは消去する.ただし,上の式を見ると \(dG = pdq - PdQ\) となっているので,基本的には \((q, Q)\) を変数にしてスタートする.そしてルジャンドル変換を通して変数を入れ替えていく.
警告
母関数 \(G\) を求めるのが目的ではなく,与えられた母関数から正準変換 \(Q = Q(q, p), P = P(q, p)\) を求めるのが目的である.
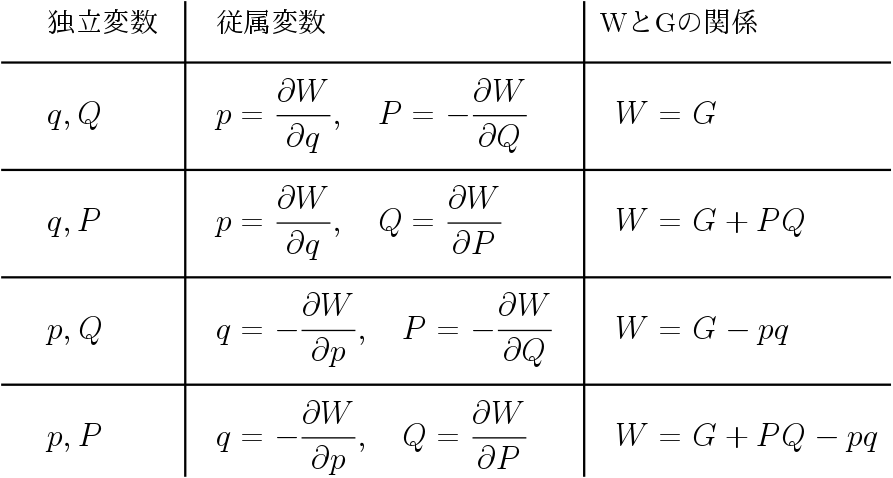
ケース1
母関数の独立変数を \(q, Q\) とする.すると
\begin{align*}
& p(q, Q) = \left. \dfrac{\partial G(q, Q)}{\partial q} \right|_{Q} \\
& P(q, Q) = \left. -\dfrac{\partial G(q, Q)}{\partial Q} \right|_{q}
\end{align*}
を得る.
警告
目的は \(Q = Q(q, p), P = P(q, p)\) を求めることである.
よってこれらを解いて \(Q = Q(q, p), q = q(Q, P)\) などを求めれば
\begin{align*}
& Q(q, p) \\
& P(q, p) = P(q, Q(q, p))
\end{align*}
より正準変換を得られる.
ケース2
母関数の独立変数を \(q, P\) とする.しかし今 \(G\) は \(q, Q\) の関数であるから,変数を \(Q \rightarrow P\) と変更する必要がある.そこでルジャンドル変換 \(W = G(q, P) + PQ\) を行う.まず始めに \(pdq = P dQ + dG\) より
\begin{align*}
pdq = P \left( \dfrac{\partial Q(q, P)}{\partial q}dq + \dfrac{\partial Q(q, P)}{\partial P}dP \right) + \dfrac{\partial G(q, P)}{\partial q}dq + \dfrac{\partial G(q, P)}{\partial P}dP
\end{align*}
よって
\begin{align*}
p = P \left. \dfrac{\partial Q}{\partial q} \right|_{P} + \left. \dfrac{\partial G}{\partial q} \right|_{P}, \quad 0 = P\left. \dfrac{\partial Q}{\partial P}\right|_{q} + \left. \dfrac{\partial G}{\partial P}\right|_{q}
\end{align*}
すると
\begin{align*}
& \left. \dfrac{\partial (G + PQ)}{\partial q}\right|_{P} = \left. \dfrac{\partial G}{\partial q}\right|_{P} + P \left. \dfrac{\partial Q}{\partial q}\right|_{P} = p \\
& \left. \dfrac{\partial (G + PQ)}{\partial P} \right|_{q} = \left. \dfrac{\partial G}{\partial P} \right|_{q} + P\left. \dfrac{\partial Q}{\partial P} \right|_{q} + Q = Q
\end{align*}
より \(p(q, P) = \partial W / \partial q\) , \(Q(q, P) = \partial W / \partial P\) を求められる.ここから \(Q(q, p), P(q, p)\) を頑張って求めれば良い.
ケース3
母関数の独立変数を \(p, Q\) とする.しかし今 \(G\) は \(q, Q\) の関数であるから,変数を \(q \rightarrow p\) と変更する.ルジャンドル変換 \(W(p, Q) = G(p, Q) - pq\) を行う.すると \(q(p, Q) = -\partial W / \partial p\) , \(P(p, Q)= - \partial W / \partial Q\) を求められる.ここから \(Q(q, p), P(q, p)\) を頑張って求めれば良い.
ケース4
母関数の独立変数を \(p, P\) とする.しかし今 \(G\) は \(q, Q\) の関数であるから,変数を \((q, Q) \rightarrow (p, P)\) と変更する必要がある.そこでルジャンドル変換 \(W = G(p, P) - pq + PQ\) を行う.すると \(q(p, P) = - \partial W / \partial p\) , \(Q(p, P) = \partial W / \partial P\) を求められる.ここから \(Q(q, p), P(q, p)\) を頑張って求めれば良い.
それぞれの場合についてGまたはWという関数を1つ指定すると変換が1つ決まる.つまり正準変換は関数の数だけ,つまり無限個ある.厳密に分類するとGが母関数であり,Wはルジャンドル変換された母関数である.
注釈
各場合において母関数は ユーザーが自由に決めて良い .
とても簡単な母関数を使ってどういう正準変換になっているかを見てみよう.
| 表の1つ目: | \(W = qQ\) とする.すると \(p = Q, P = -q\) が得られる.よって正準変換は \(Q = p, P = -q\) である.これはq,pの立場を入れ変える変換である. |
|---|
| 表の2つ目: | \(W = qP\) とする.すると \(p = P, Q = q\) となる.これは恒等変換である.この場合 \(G = W - PQ = 0\) であるから,ラグランジアンのずれはない.よって作用は不変である. |
|---|
| 表の2つ目: | \(W = qp + \epsilon \mathcal{G}(q, P)\) とする.これは ポアソン括弧を使って無限小変換を記述する で述べた無限小変換になる. |
|---|
| 表の2つ目: | \(W = Pf(q)\) とする.すると \(p = P \dfrac{df}{dq}, Q = f(q)\) となる.これはラグランジュ形式における点変換である. \(dQ = \dfrac{df}{dq}dq, P = \dfrac{dq}{df}p\) と変換することにより \(p\dot{q} = P\dot{Q}\) が成立する.よってこの場合も作用は不変である. |
|---|
| 表の3つ目: | \(W = pQ\) とする.すると \(q = -Q,, P = -p\) となる.よって正準変換は \(Q = -q, P = -p\) である.これは座標と運動量座標の符号を一斉に反転する変換である. |
|---|
ハミルトンヤコビ方程式のところで必要になるためここでやっておく必要がある.次に正準変換が
\begin{align*}
Q = Q(q, p, t), \quad P = P(q, p, t)
\end{align*}
のように時間に依存している場合を考える.
時間に依存する変換の場合ハミルトニアンの値も変換するので, \(H \rightarrow K\) と変化したとしよう. つまり \((q, Q)\) を独立変数にとって
\begin{align*}
p(q, Q, t)\dot{q} - H(q, p(q, Q, t), t) = P(q, Q, t)\dot{Q} - K(Q, P(q, Q, t), t) + \dfrac{dG(q, Q, t)}{dt}
\end{align*}
が作用に関する等式である.dG/dtを展開すると
\begin{align*}
p\dot{q} - H = P\dot{Q} - K + \left. \dfrac{\partial G}{\partial q} \right|_{Q, t} + \left. \dfrac{\partial G}{\partial Q} \right|_{q, t} + \left. \dfrac{\partial G}{\partial t} \right|_{q, Q}
\end{align*}
となる.各係数を比較すると
\begin{align*}
& p = \left. \dfrac{\partial G}{\partial q} \right|_{Q, t} \\
& P = -\left. \dfrac{\partial G}{\partial Q} \right|_{q, t} \\
& K = H + \left. \dfrac{\partial G}{\partial t} \right|_{q, Q}
\end{align*}
となる.正準変換の表 で \(H \rightarrow K = H + \partial W / \partial t\) となること以外に変化はない.
1変数の場合から,ポアソン括弧が保存するのであればそれは正準変換だ,と分かったので,多変数の場合についてもポアソン括弧が保存するものを正準変換とする.つまりN次元において \((q_i, p_i) (i = 1, 2, \cdots, N)\) から \((Q_{i}(q_{*}, p_{*}), P_{i}(q_{*}, p_{*})) (i = 1, 2, \cdots, N)\) へと変換されたとする.物理量A,Bのポアソン括弧をそれぞれの座標系で表した
\begin{align*}
\{ A, B \}_{Q, P} = \sum_{i}\left( \dfrac{\partial A}{\partial Q_i}\dfrac{\partial B}{\partial P_i} - \dfrac{\partial B}{\partial Q_i}\dfrac{\partial A}{\partial P_i} \right)
\end{align*}
及び
\begin{align*}
\{ A, B \}_{q, p} = \sum_{i}\left( \dfrac{\partial A}{\partial q_i}\dfrac{\partial B}{\partial p_i} - \dfrac{\partial B}{\partial q_i}\dfrac{\partial A}{\partial p_i} \right)
\end{align*}
が等しくなる条件を求める.ここでも詳しい計算は省く.ポアソン括弧が保存する条件は
\begin{align*}
\{ Q_j, Q_k \}_{q, p} = 0, \quad \{ P_j, P_k\}_{q, p} = 0, \quad \{ Q_j, P_k\}_{q, p} = \delta_{jk}
\end{align*}
である.
母関数を用いる正準変換は,多変数の場合も同様に行える. \((q_{*}, Q_{*})\) を独立変数とする母関数だと
\begin{align*}
\sum_{i}p_i \dot{q}_i - H = \sum_{i}P_i \dot{Q}_i - K + \dfrac{dG}{dt}
\end{align*}
から
\begin{align*}
p_i = \dfrac{\partial G}{\partial q_i}, \quad P_i = \dfrac{\partial G}{\partial Q_i}, \quad K = H + \dfrac{\partial G}{\partial t}
\end{align*}
が得られる.これらから \((Q_{i}(q_{*}, p_{*}), P_{i}(q_{*}, p_{*})) (i = 1, 2, \cdots, N)\) を求めれば良い.
\(q_{*}, P_{*}\) を独立変数にとって,点変換を引き起こす母関数 \(W = \sum_{i}P_i f_{i}(q_{*})\) を用いると,きちんと
\begin{align*}
Q_i = f_{i}(q_{*}), \quad p_i = \sum_{j}P_j \dfrac{\partial f_{j}(q_{*})}{\partial q_i}
\end{align*}
が得られる.