最初のうちは「何でこんなことをしないといけないのか」という風に感じてしまいがちであるが,ハミルトン形式のご利益があるのはポアソン括弧や正準変換を行うところにある.もうひとつ重要なのは,位相空間での軌道は絶対に交差しないということだ.
以下のような量が時間的に保存すること(が多い)ことは今まで述べてきた.
\begin{align*}
H = \sum_{i}p_{i}\dot{q}_{i} - L
\end{align*}
これをハミルトニアンと呼ぶ.これは \(q, p\) の関数だと思えば
\begin{align*}
H(q, p) = \sum_{i}p_{i}\dot{q}_{i}(q, p) - L({q}, {\dot{q}(q, p)})
\end{align*}
\(q, \dot{q}\) の関数だと思えば
\begin{align*}
H(q, p(q, \dot{q})) = \sum_{i}p_{i}(q, \dot{q})\dot{q} - L(q, \dot{q})
\end{align*}
である.この計算はルジャンドル変換になっているので
\begin{align*}
-\left. \dfrac{\partial H}{\partial q_i} \right|_{q^i, p} = \left. \dfrac{\partial L}{\partial q_i} \right|_{q^i, \dot{q}}
\end{align*}
が成立する.ここで左辺と右辺の偏微分の意味は以下の通りである.
- \(p_{*}, q_{*}\) のうち \(q_i\) 以外を一定にして \(-H(q_{*}, p_{*})\) を偏微分したもの
- \(q_{*}, \dot{q}_{*}\) のうち \(q_i\) 以外を一定にして \(L(q_{*}, \dot{q}_{*})\) 偏微分したもの
ただし偏微分の一定にする記号のうち上付きになっているものは,それ以外を一定にするという意味である.
これが成立するようにルジャンドル変換をしている.これによりオイラーラグランジュ方程式は
\begin{align*}
\begin{cases} \dfrac{d q_i}{dt} = \left. \dfrac{\partial H}{\partial p_i} \right|_{p^i, q_{*}} \\ \dfrac{dp_i}{dt} = -\left. \dfrac{\partial H}{\partial q_i} \right|_{q^i, p_{*}} \end{cases}
\end{align*}
へと書き換えられる.
この方程式は以下のような形に書き換えられる.
\begin{align*}
\begin{pmatrix} \dfrac{dq}{dt} \\ \dfrac{dp}{dt} \end{pmatrix} = \begin{pmatrix} 0 & 1 \\ -1 &0 \end{pmatrix} \begin{pmatrix} \dfrac{\partial H}{\partial q} \\ \dfrac{\partial H}{\partial p} \end{pmatrix}
\end{align*}
この行列は90度の回転行列であるから,各点においてハミルトニアンの勾配に直角に「流れ」を生み出している.
オイラーラグランジュ方程式はラグランジアンの変分の停留を求めることで得られた.そこでハミルトニアンの定義に基づいたラグランジアン
\begin{align*}
\sum_{i}p_{i}\dot{q}_{i} - H(p_{*}, q_{*})
\end{align*}
を停留させる経路を求めることで正準方程式を導出してみる.
独立変数は \(q_{*}, p_{*}\) であるから,これらの変分
\begin{align*}
\delta I = \int \left( \sum_{i}(p_i + \delta p_i)(\dot{q}_i + \delta \dot{q}_i - p_{i}\dot{q}_{i}) - H(p_{*} + \delta p_{*}, q_{*} + \delta q_{*}) + H(p_{*}, q_{*}) \right) dt
\end{align*}
を計算していくと
\begin{align*}
\int \left( \sum_{i} \left( \delta q_{i}\left( -\dot{p}_{i} - \dfrac{\partial H}{\partial q_i}\right) + \delta p_{i}\left( \dot{q}_{i} - \dfrac{\partial H}{\partial p_i} \right) \right) + \dfrac{d(p_{i}\delta q_{i})}{dt}\right) dt
\end{align*}
となる.最後の項は表面項であるから(停留値にオフセットをのせるだけ)無視できて,変分に関する項の係数をゼロとみなすことで正準方程式を得ることができる.
座標 \(q\) と運動量座標 \(p\) の2組の 独立な 変数 \((q, p)\) からなる空間を位相空間と呼ぶ.これに対して \((t, q)\) が表す曲線を配位空間と呼ぶ.
運動は初期座標 \(q(t_i)\) と初期速度 \(\dot{q}(t_i)\) を決めると一意的に決まる.当然同じ場所にいても初期速度が違えばその後の運動は異なる.そのため配位空間における運動を表現するグラフは交差する可能性がある.一方位相空間における運動は グラフが交差しない .今からその理由の説明を行う.
正準方程式より位相空間における速度ベクトルは
\begin{align*}
\left( \dfrac{\partial H}{\partial q}, \dfrac{\partial H}{\partial p} \right) = \left( \dfrac{\partial H}{\partial p}, -\dfrac{\partial H}{\partial q} \right)
\end{align*}
であるから,位相空間においてHが変化する方向である \(\nabla H\) を90度回転させた方向である.よってHが変化する方向とは直角に移動する時,Hは変化しない.実際
\begin{align*}
H\left( q + \epsilon \dfrac{\partial H}{\partial p}, p - \epsilon \dfrac{\partial H}{\partial q} \right) = H(q, p) + \dfrac{\partial H}{\partial q} \cdot \epsilon \dfrac{\partial H}{\partial p} + \dfrac{\partial H}{\partial p} \cdot (-\epsilon) \dfrac{\partial H}{\partial q} = H(q, p)
\end{align*}
である.これに関連してこの速度ベクトルの発散はゼロである.
\begin{align*}
\mathrm{div} \left( \dfrac{\partial H}{\partial p}, -\dfrac{\partial H}{\partial q} \right) = \dfrac{\partial}{\partial q}\left( \dfrac{\partial H}{\partial p} \right) + \dfrac{\partial}{\partial p}\left( -\dfrac{\partial H}{\partial q} \right) = 0
\end{align*}
位相空間内で表した運動
位相空間において以下の時間微分演算子は
\begin{align*}
\dfrac{d}{dt} = \dfrac{\partial H}{\partial p}\dfrac{\partial}{\partial q} - \dfrac{\partial H}{\partial q}\dfrac{\partial}{\partial p}
\end{align*}
とかける.これは \(\partial / \partial q\) , \(\partial / \partial p\) を速度ベクトルの基底とみなすと各係数がその速度成分を表しているとも読める(微分幾何学的な考え方).
この演算子
\begin{align*}
\dfrac{d}{dt} = \dfrac{\partial H}{\partial p}\dfrac{\partial}{\partial q} - \dfrac{\partial H}{\partial q}\dfrac{\partial}{\partial p}
\end{align*}
は多変数についても成立する. \(\partial / \partial q\) は \(q\) 方向の方向微分成分, \(\partial / \partial p\) は \(p\) 方向の方向微分成分である.
交差しない理由
このようにして位相空間における速度は位置の関数になっている.そのためある場所における速度は1つしかない.そこで各点における速度を接続していくと位相空間全体を結ぶ「流れ」のようなものができる.これらの「流れ」は「起こりうる運動全ての軌道」を表している.そしてこれらの軌道に交差があったとしよう.すると交差点においては2つの別々の方向に流れが分岐して存在していることになるため,正準方程式に矛盾する.そのため,位相空間におけるハミルトニアンフローは絶対に交差しない.
注釈
つまりハミルトニアンフローは積分曲線である.
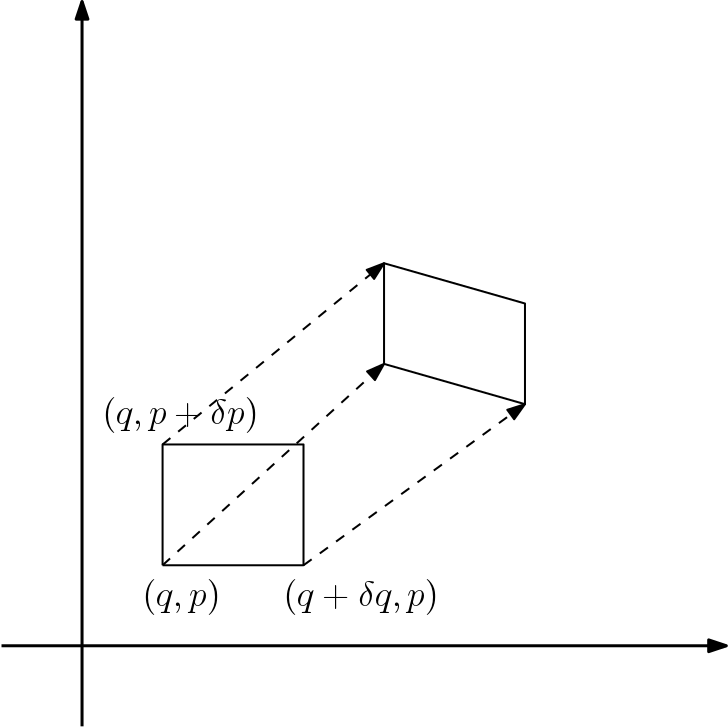
今ある位相空間に \(q_i, q_i + \delta q_i\) , \(p_i, p_i + \delta p_i\) で囲まれた長方形の領域があるとする.時間が経過するとこの長方形領域も流されていく.この領域が変化しないというのがリウヴィルの定理である.
始め \((q, p)\) にいた粒子は \(\delta t\) 後には
\begin{align*}
\left( q + \dfrac{dq}{dt}\delta t, p + \dfrac{dp}{dt}\delta t \right) = \left( q + \dfrac{\partial H(q, p)}{\partial p}\delta t, p - \dfrac{\partial H(q, p)}{\partial q}\delta t \right)
\end{align*}
へと流される.同様に \((q + \delta q, p)\) にいた粒子は
\begin{align*}
& (q + \delta q + \dfrac{\partial H(q + \delta q, p)}{\partial p}\delta t, p - \dfrac{\partial H(q + \delta q, p)}{\partial q}\delta t) \\
&= \left( q + \delta q + \dfrac{\partial H(q, p)}{\partial p}\delta t + \dfrac{\partial^2 H(q, p)}{\partial q \partial p}\delta q \delta t, p - \dfrac{\partial H(q, p)}{\partial q}\delta t - \dfrac{\partial^2 H(q, p)}{\partial q^2}\delta q \delta t \right)
\end{align*}
へと流される.
始め \((\delta q, 0)\) だったずれが
\begin{align*}
\left( \delta q + \dfrac{\partial^2 H(q, p)}{\partial q \partial p}\delta q \delta t, -\dfrac{\partial^2 H(q, p)}{\partial q^2}\delta q \delta t \right)
\end{align*}
へと変化している.同様に \((q, p + \delta p)\) の場所にいた粒子に対しては
\begin{align*}
\left( \dfrac{\partial^2 H(q, p)}{\partial p^2}\delta p \delta t, \delta p - \dfrac{\partial^2 H(q, p)}{\partial q \partial p}\delta p \delta t \right)
\end{align*}
である.これらの外積を計算すると
\begin{align*}
\left( \delta q + \dfrac{\partial^2 H(q, p)}{\partial q \partial p}\delta q \delta t \right) \left( \delta p - \dfrac{\partial^2 H(q, p)}{\partial q \partial p}\delta p \delta t \right) - \left( -\dfrac{\partial^2 H(q, p)}{\partial q^2}\delta q \delta t \right)\left( \dfrac{\partial^2 H(q, p)}{\partial p^2}\delta p \delta t \right) = \delta q \delta p
\end{align*}
位相空間における関数 \(A(q, p)\) の時間微分を考えると
\begin{align*}
\dfrac{d}{dt}A(q, p) = \sum_{i}\left( \dot{q}_{i}\dfrac{\partial A(q, p)}{\partial q_i} + \dot{p}_{i}\dfrac{\partial A(q, p)}{\partial p_i} \right) + \dfrac{\partial A}{\partial t}
\end{align*}
正準方程式を代入すると
\begin{align*}
\dfrac{d}{dt}A(q, p) = \sum_{i}\left( \dfrac{\partial A(q, p)}{\partial q_i}\dfrac{\partial H(q, p)}{\partial p_i} - \dfrac{\partial H(q, p)}{\partial q_i} \dfrac{\partial A(q, p)}{\partial p_i} \right) + \dfrac{\partial A}{\partial t}
\end{align*}
となる.ここで以下のポアソン括弧という演算を代入する.
\begin{align*}
\{ A, B \} = \sum_{i}\left( \dfrac{\partial A}{\partial q_i}\dfrac{\partial B}{\partial p_i} - \dfrac{\partial B}{\partial q_i}\dfrac{\partial A}{\partial p_i} \right)
\end{align*}
すると正準方程式は
\begin{align*}
\begin{cases} \dfrac{dq}{dt} = \{ q, H \} \\ \dfrac{dp}{dt} = \{ p, H \} \end{cases}
\end{align*}
と表される.このことから,ハミルトニアンとのポアソン括弧は時間微分と等価である といえる.
ポアソン括弧の性質
主に以下のような性質を持つ.
\begin{align*}
\{ A, B \} = -\{ B, A \}
\end{align*}
\begin{align*}
& \{ A, \{ B, C \} \} + \{ B, \{ A, C \} \} + \{ C, \{ A, B \} \} = 0 \\
& \{ A, \{ B, C \} \} = \{ \{ A, B \}, C \} \{ \{ A, C \}, B \}
\end{align*}
\begin{align*}
& \{ A, p_j \} = \dfrac{\partial A}{\partial q_j} \\
& \{ A, q_j \} = -\dfrac{\partial A}{\partial p_j}
\end{align*}
上でハミルトニアンとの 右からのポアソン括弧は時間微分である と述べたように,基本的にポアソン括弧は 右側から掛けるものである .
ポアソン括弧が0になることの意味
ヤコビ恒等式の意味から考える.\(A\) という物理量に対して
- 右から \(B\) とのポアソン括弧をとる.\(\{A, B \}\)
- さらに右から \(C\) とのポアソン括弧をとる. \(\{ \{A, B \}, C \}\)
で得られた量と
- 右から \(C\) とのポアソン括弧をとる. \(\{A, C \}\)
- さらに右から \(B\) とのポアソン括弧をとる. \(\{ \{A, C \}, B \}\)
の差をとるとそれは
\begin{align*}
\{ A, \{ B, C \} \} = \{ \{ A, B \}, C \} - \{ \{ A, C \}, B \}
\end{align*}
よってもし \(\{ B, C \} = 0\) ならば上に挙げた2つの操作は同じ結果を出す.このようにポアソン括弧が0になる量の組を,ポアソン括弧の意味で可換であるという.
例としてハミルトニアンに \(q_i\) が含まれない場合,つまり循環座標である場合を考えよう.すると以下のように \(p_i\) と \(H\) はポアソン可換となる.
\begin{align*}
\{ p_i, H \} = \{ H, p_i \} = 0
\end{align*}
これには物理的には2通りの解釈が可能である.
- \(p_i\) について右から \(H\) とのポアソン括弧をとった結果,つまり \(p_i\) の時間変化はゼロである.これは \(q_i\) が循環座標であれば \(p_i\) が保存量であるということを言っている.
- \(H\) について右から \(p_i\) とのポアソン括弧をとった結果,つまり \(H\) の \(q_i\) 方向の微分はゼロである.これはハミルトニアンが \(q_i\) 方向に不変であるということを言っている.